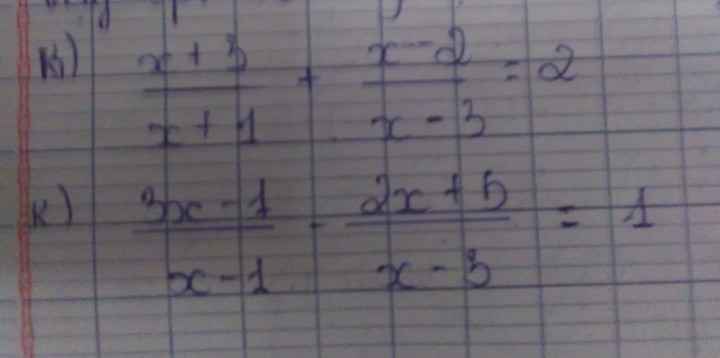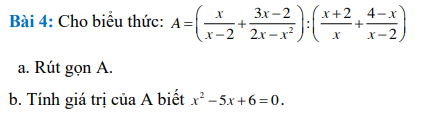Lời giải:
ĐKXĐ: $x\neq 3$
PT $\Leftrightarrow \frac{x(x+4)}{x^3-27}=\frac{x+3}{x^2+3x+9}-\frac{1}{3-x}=\frac{x+3}{x^2+3x+9}+\frac{1}{x-3}=\frac{(x+3)(x-3)+(x^2+3x+9)}{(x^2+3x+9)(x-3)}=\frac{2x^2+3x}{x^2-27}$
$\Rightarrow x(x+4)=2x^2+3x$
$\Leftrightarrow x^2-x=0$
$\Leftrightarrow x(x-1)=0$
$\Rightarrow x=0$ hoặc $x=1$ (tm)

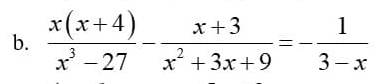 giúp mình với ạ
giúp mình với ạ




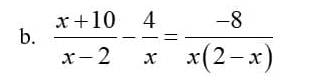 giúp mình với ạ
giúp mình với ạ