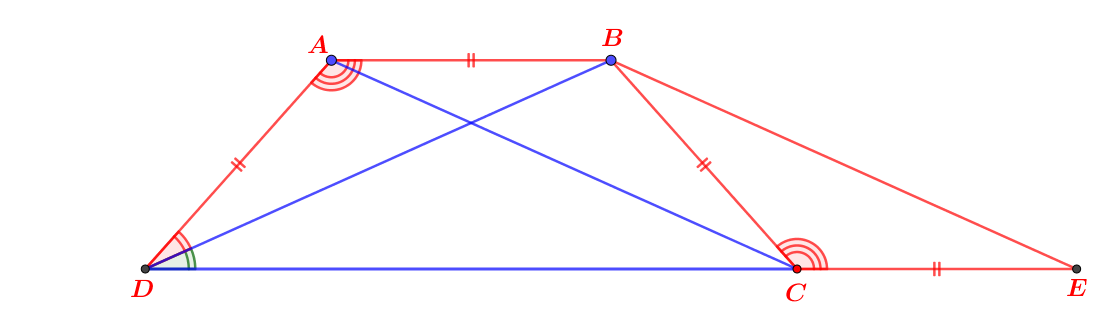
Bài 8. Cho hình thang cân ABCD (AB//CD) có ,AD=AB
a. Chứng minh rằng: BD là tia phân giác của góc ADC.
b. Chứng minh: BD⊥BC
Bài 9. Cho tam giác ABC cân ở A có M là trung điểm của BC. Trên tia AM lấy N. BN cắt AC ở D, CN cắt AB ở E. Chứng minh BEDC là hình thang cân.
Bài 8. Cho hình thang cân ABCD (AB//CD) có ,AD=AB
a. Chứng minh rằng: BD là tia phân giác của góc ADC.
b. Chứng minh: BD⊥BC
Bài 9. Cho tam giác ABC cân ở A có M là trung điểm của BC. Trên tia AM lấy N. BN cắt AC ở D, CN cắt AB ở E. Chứng minh BEDC là hình thang cân.
Bài 8. Cho hình thang cân ABCD (AB//CD) có ,AD=AB
a. Chứng minh rằng: BD là tia phân giác của góc ADC.
b. Chứng minh: BD⊥BC
Bài 9. Cho tam giác ABC cân ở A có M là trung điểm của BC. Trên tia AM lấy N. BN cắt AC ở D, CN cắt AB ở E. Chứng minh BEDC là hình thang cân.
Bài 8. Cho hình thang cân ABCD (AB//CD) có ,AD=AB
a. Chứng minh rằng: BD là tia phân giác của góc ADC.
b. Chứng minh: BD⊥BC
Bài 9. Cho tam giác ABC cân ở A có M là trung điểm của BC. Trên tia AM lấy N. BN cắt AC ở D, CN cắt AB ở E. Chứng minh BEDC là hình thang cân.
Bài 8. Cho hình thang cân ABCD (AB//CD) có ,AD=AB
a. Chứng minh rằng: BD là tia phân giác của góc ADC.
b. Chứng minh: BD⊥BC
Bài 9. Cho tam giác ABC cân ở A có M là trung điểm của BC. Trên tia AM lấy N. BN cắt AC ở D, CN cắt AB ở E. Chứng minh BEDC là hình thang cân.
Bài 8. Cho hình thang cân ABCD (AB//CD) có ,AD=AB
a. Chứng minh rằng: BD là tia phân giác của góc ADC.
b. Chứng minh: BD⊥BC
Bài 9. Cho tam giác ABC cân ở A có M là trung điểm của BC. Trên tia AM lấy N. BN cắt AC ở D, CN cắt AB ở E. Chứng minh BEDC là hình thang cân.
Bài 8. Cho hình thang cân ABCD (AB//CD) có ,AD=AB
a. Chứng minh rằng: BD là tia phân giác của góc ADC.
b. Chứng minh: BD⊥BC
Bài 9. Cho tam giác ABC cân ở A có M là trung điểm của BC. Trên tia AM lấy N. BN cắt AC ở D, CN cắt AB ở E. Chứng minh BEDC là hình thang cân.
Bài 8. Cho hình thang cân ABCD (AB//CD) có ,AD=AB
a. Chứng minh rằng: BD là tia phân giác của góc ADC.
b. Chứng minh: BD⊥BC
Bài 9. Cho tam giác ABC cân ở A có M là trung điểm của BC. Trên tia AM lấy N. BN cắt AC ở D, CN cắt AB ở E. Chứng minh BEDC là hình thang cân.
Bài 8. Cho hình thang cân ABCD (AB//CD) có ,AD=AB
a. Chứng minh rằng: BD là tia phân giác của góc ADC.
b. Chứng minh: BD⊥BC
Bài 9. Cho tam giác ABC cân ở A có M là trung điểm của BC. Trên tia AM lấy N. BN cắt AC ở D, CN cắt AB ở E. Chứng minh BEDC là hình thang cân.
Bài 8. Cho hình thang cân ABCD (AB//CD) có ,AD=AB
a. Chứng minh rằng: BD là tia phân giác của góc ADC.
b. Chứng minh: BD⊥BC
Bài 9. Cho tam giác ABC cân ở A có M là trung điểm của BC. Trên tia AM lấy N. BN cắt AC ở D, CN cắt AB ở E. Chứng minh BEDC là hình thang cân.
giúp mik vs ạ mik cho 5 sao