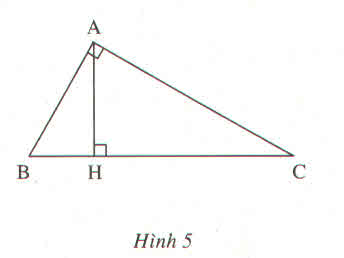
Áp dụng định lí Pytago vào ΔACH vuông tại H, ta được:
\(AC^2=CH^2+AH^2\)
\(\Leftrightarrow AH^2=AC^2-CH^2=20^2-16^2=144\)
hay AH=12(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow HB=\dfrac{AH^2}{HC}=\dfrac{12^2}{16}=9\left(cm\right)\)
Ta có: BC=BH+CH(H nằm giữa B và C)
nên BC=9+16=25(cm)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AB^2=BC^2-AC^2=25^2-20^2=225\)
hay AB=15(cm)
Vậy: AB=15cm; AH=12cm; BC=25cm; BH=9cm
Đúng 1
Bình luận (0)
