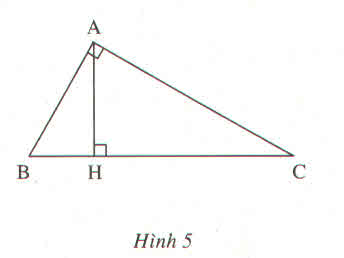
Xét tam giác ABC vuông tại A, đường cao AH
Theo định lí Pytago tam giác ABC vuông tại A
\(BC=\sqrt{AB^2+AC^2}=\sqrt{481}\)
* Áp dụng hệ thức : \(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{15.16}{\sqrt{481}}=\dfrac{240}{\sqrt{481}}=\dfrac{240\sqrt{481}}{481}\)cm
* Áp dụng hệ thức : \(AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{225}{\sqrt{481}}=\dfrac{225\sqrt{481}}{481}\)cm
=> \(HC=BC-BH=\sqrt{481}-\dfrac{225\sqrt{481}}{481}\)cm
Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
hay \(BC=\sqrt{481}\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{225\sqrt{481}}{481}\left(cm\right)\\CH=\dfrac{256\sqrt{481}}{481}\left(cm\right)\\AH=\dfrac{240\sqrt{481}}{481}\left(cm\right)\end{matrix}\right.\)