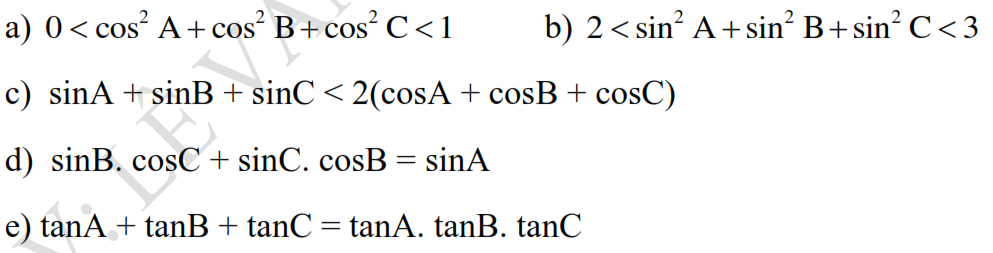Xét tam giác ABC và tam giác AEF có:
\(\widehat{BAC}\) chung
\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\left(=cosBAC\right)\)
\(\Rightarrow\Delta ABC\sim\Delta AEF\left(c.g.c\right)\)
\(\Rightarrow\dfrac{EF}{BC}=\dfrac{AE}{AB}=cosBAC\)
Ta có \(\left\{{}\begin{matrix}\widehat{BAC}.chung\\\widehat{AEB}=\widehat{AFC}\left(=90^0\right)\end{matrix}\right.\) nên \(\Delta AFC\sim\Delta AEB\left(g.g\right)\)
\(\Rightarrow\dfrac{AE}{AF}=\dfrac{AB}{AC}\Rightarrow\Delta AEF\sim\Delta ACB\left(c.g.c\right)\\ \Rightarrow\dfrac{AE}{AC}=\dfrac{EF}{BC}\)
Mà \(\cos BAC=\dfrac{AE}{AC}\) nên ta đc đpcm