Chương I - Hệ thức lượng trong tam giác vuông
Các câu hỏi tương tự
Cho tam giác ABC có ba góc nhọn ( AB >AC), kẻ đường cao
AD, BE cắt nhau tại H. CH cắt AB tại F.
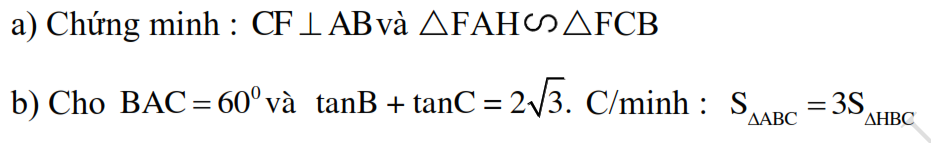
cho tam giác ABC nhọn , đường cao AD,BE,EF cắt nhau tại H . CM:\(\dfrac{FE}{BC}=cosBAC\)
Cho tam giác nhọn abc các đường cao AD, BE, CF cắt nhau tại H, gọi O là trung điểm của BC, I là trung điểm của AH, K là giao điểm của EF, OI .
Chứng minh AH^2= 4.IK.IO
Cho \(\Delta ABC\) có 3 góc nhọn; đường cao AH, BE, CF cắt nhau ở H.
a) C/m \(BH.BE+HC.EC=BC^2\)
b) C/m \(\dfrac{HD}{AD}+\dfrac{HE}{BE}+\dfrac{HF}{CF}=1\)
c) C/m H là giao điểm của các đường phân giác của \(\Delta DEF\)
Cho tam giác ABC nhọn , các đường cao AD,BE,CF cắt nhau tại H . cmr : HA/BC + HB/AC + HC/AB >= \(\sqrt{3}\)
* Cho tam giác nhọn ABC có hai đường cao BD và CE cắt nhau tại H. Trên HB và HC lần lượt lấy điểm M,N sao cho góc AMC= góc ANB= \(90^0\). Chứng minh:AM=AN
* Cho tam giác ABC vuông tại A, đường cao AH. Biết \(\dfrac{AB}{AC}=\dfrac{20}{21}\)và AH=420. Tính chu vi tam giác ABC
Cho tam giác nhọn ABC, AB < AC, đường cao AD. Gọi E, F lần lượt là hình chiếu vuông góc của D trên AB, AC.
Xem chi tiết
c) Chứng minh: \(tan^3C=\dfrac{BE}{CF}\)
Cho tam giác abc nhọn hai đường cao BD, CE gặp nhau tại F. Đường tròn đường kính CF cắt BC tại điểm thứ hai là G. Chứng minh A, F, G thẳng hàng
Bài 1:
Cho ΔABC nhọn, hai đường cao AD và BE cắt nhau tại H, chứng minh: AD = DH.tanB.tanC
Bài 2:
Cho ΔABC nhọn có ∠C = 60o , AC = 8cm, kẻ đường cao AH.
a, Giải ΔABC
b, Tia phân giác của ACB cắt AH tại I. Tính diện tích tam giác AIC?
HELP!!!