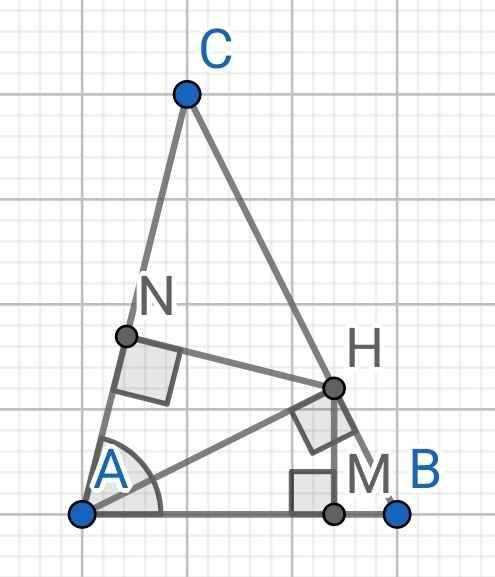
Do M, N lần lượt là hình chiếu của H lên AB, AC
⇒ HM ⊥ AB và HN ⊥ AC
∆AHB vuông tại H có HM là đường cao
⇒ AH² = AM.AB (1)
∆AHC vuông tại C có HN là đường cao
⇒ AH² = AN.AC (2)
Từ (1) và (2) ⇒ AM.AB = AN.AC

Do M, N lần lượt là hình chiếu của H lên AB, AC
⇒ HM ⊥ AB và HN ⊥ AC
∆AHB vuông tại H có HM là đường cao
⇒ AH² = AM.AB (1)
∆AHC vuông tại C có HN là đường cao
⇒ AH² = AN.AC (2)
Từ (1) và (2) ⇒ AM.AB = AN.AC
Cho tam giác ABC nhọn có AB> AC. Gọi M là tđ của BC; H là trực tâm; AD,BE,CF là các đường cao của tam giác ABC. Kí hiệu (C1) và ( C2) lần lượt là đường tròn ngoại tiếp tam giác AEF và DKE, với K là giao điểm của EF và BC.CMR: ME là tiếp tuyến chung của (C1) và (C2).
Giúp em với ạ!!
Cho tam giác ABC nhọn, đường cao AH. Gọi M, N lần lượt là hình chiếu của H trên AB, AC
a) C/m tam giác AMN đồng dạng với tam giác ACB
b) C/m AH = \(\dfrac{BC}{cotB+cotC}\)
c) \(S_{AMN}\)= \(sin^2B.sin^2C\). \(S_{ABC}\)
Các bạn có thể giúp mình bài này không ạ? Mình cảm ơn rất nhiều!
Cho tam giác ABC vuông tại A (AB >AC )đường tròn tâm O đường kính AB cắt BC tại H. Gọi K là trung điểm của AC a,Chứng minh AH là đường cao của tam giác ABC b, Chứng minh tam giác KOH = tam giác KAO . Suy ra số đo KHI
các bạn giải hộ mình với ạ, xin cảm ơn(mình đang cần gấp :<)
Cho tam giác ABC đều, đường cao AD, trực tâm H. M là điểm bất kỳ trên cạnh BC. Gọi E, F thứ tự là hình chiếu của M trên AB và AC. Gọi I là trung điểm của AM. ID cắt EF tại K. a) DEIF là hình gì? b) CM: M, K, H thẳng hàng. c) Xác định vị trí của M trên BC để EF đạt GTNN. d) Tìm GTNN của SDEIF biết tam giác ABC có cạnh bằng a. e) Tìm quỹ tích điểm K
help me giải vs
Cho ∆ ABC vuông tại A, có AB = 6cm, AC = 8 cm, đường cao AH, a) Giải tam giác ABC b) Chứng minh ba đỉnh A, H, C cùng thuộc đường tròn và chỉ ra tâm của đường tròn đó.
giúp tui câu này đc ko chiều tui thi r cho tam giác ABC cân tại A nội tiếp đường tròn (O). vẽ trung tuyến AM của tam giác ABC. gọi B' đối xứng với B qua O .Vẽ qua A vuông góc với CB' và cắt BC' tại H chứng minh AH là tiếp tuyến của đường tròn (O)
Cho tam giác ABC vuông tại A .Vẽ AH vuông góc BC .Gọi E, F lần lượt là hình chiếu của H trên AB và AC
Chứng minh \(\frac{AF.AC}{EF.BC}\)=\(\frac{AE}{AC}\)