c.
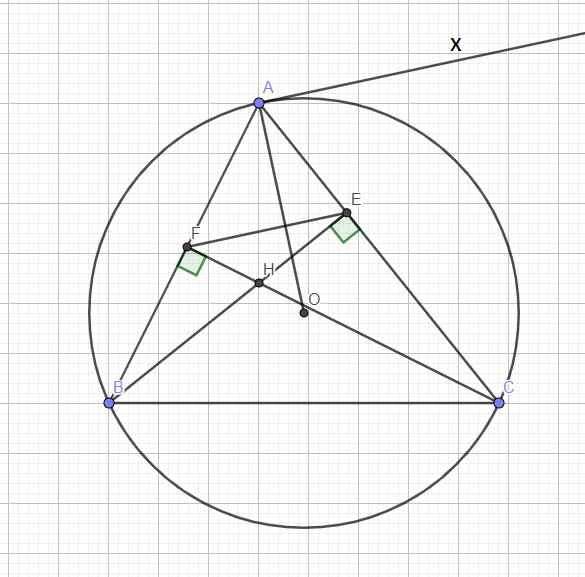
Qua A kẻ tiếp tuyến \(Ax\Rightarrow Ax\perp OA\) (1)
Do E và F cùng nhìn BC dưới 1 góc vuông
\(\Rightarrow\) Tứ giác BCEF nội tiếp
\(\Rightarrow\widehat{CEF}+\widehat{CBF}=180^0\)
Mà \(\widehat{CEF}+\widehat{AEF}=180^0\)
\(\Rightarrow\widehat{CBF}=\widehat{AEF}\)
Lại có \(\widehat{CBF}=\widehat{CAx}\) (cùng chắn AC)
\(\Rightarrow\widehat{AEF}=\widehat{CAx}\)
\(\Rightarrow Ax||EF\) (hai góc so le trọng bằng nhau) (2)
\(\left(1\right);\left(2\right)\Rightarrow OA\perp EF\)