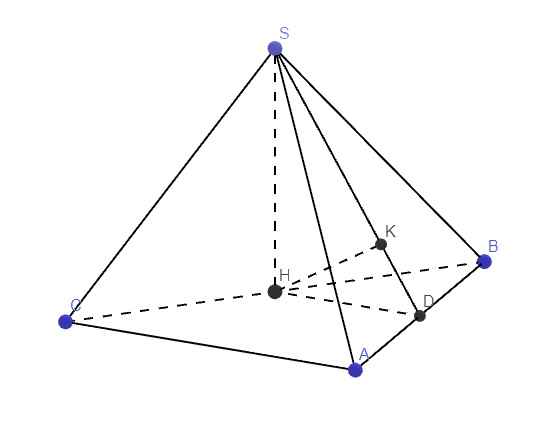
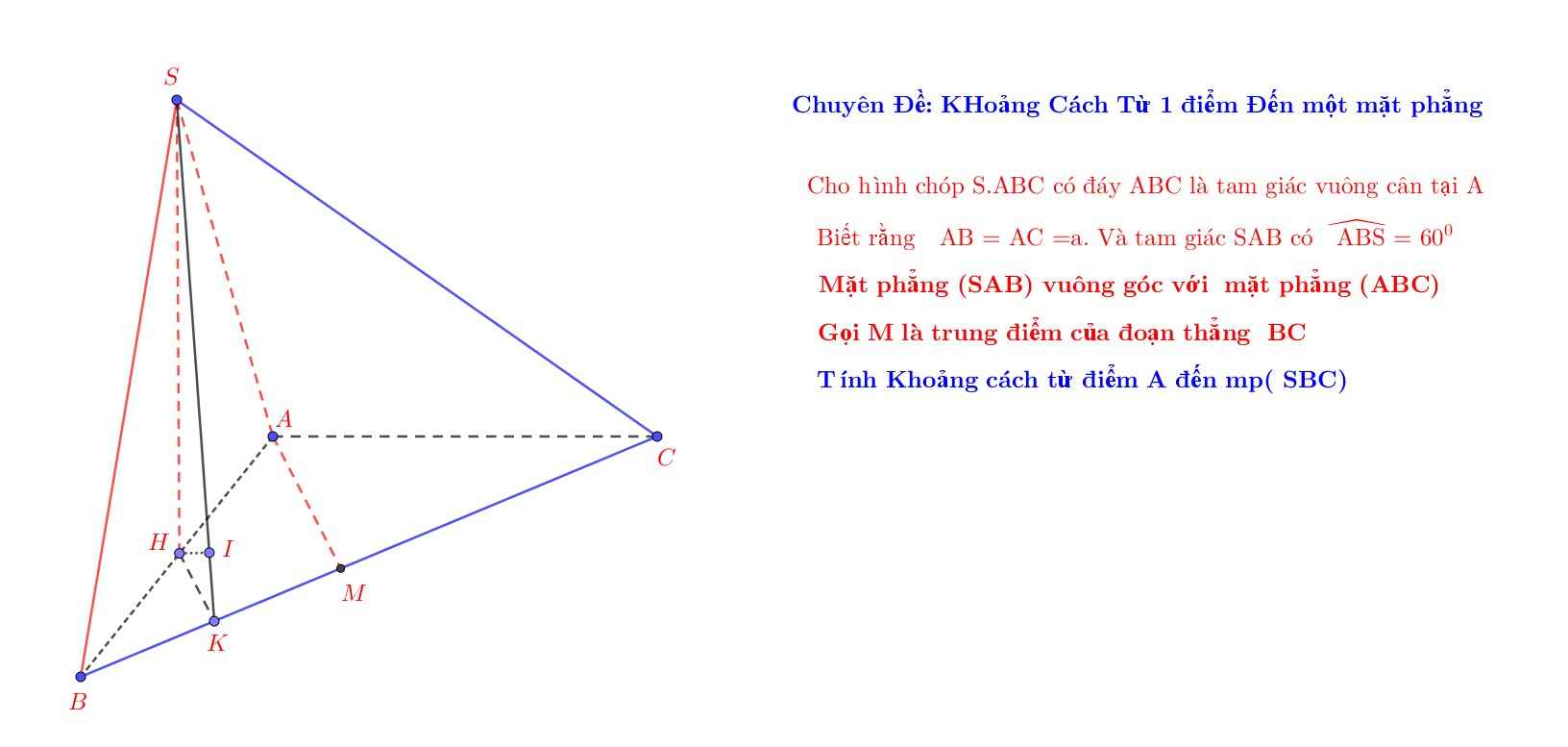
Gọi D là trung điểm AB \(\Rightarrow HD\) là đường trung bình tam giác ABC
\(\Rightarrow\left\{{}\begin{matrix}HD||AC\Rightarrow HD\perp AB\\HD=\dfrac{1}{2}AC=\dfrac{a}{2}\end{matrix}\right.\)
\(\Rightarrow AB\perp\left(SHD\right)\)
\(\Rightarrow\widehat{SDH}\) là góc giữa (SAB) và đáy
\(\Rightarrow\widehat{SDH}=60^0\)
\(\Rightarrow SH=DH.tan60^0=\dfrac{a\sqrt{3}}{2}\)
Từ H kẻ \(HK\perp SD\) (K thuộc SD)
\(\Rightarrow HK\perp\left(SAB\right)\Rightarrow HK=d\left(H;\left(SAB\right)\right)\)
\(HK=\dfrac{SH.DH}{\sqrt{SH^2+DH^2}}=\dfrac{a\sqrt{3}}{4}\)