Question

Cho ΔABC cân ở A (∠A < 90o). Vẽ BH ⊥ AC (H ∈ AC), CK ⊥ AB (K ∈ AB).

a) Chứng minh rằng AH = HK

b) Gọi I là giao điểm của BH và CK. Chứng minh rằng AI là tia phân giác của góc A

c) Chứng minh : AI vuông góc BC

d) Chứng minh : AI đi qua trung điểm M của BC

LÀM ƠN MỌI NGƯỜI GIÚP MÌNH VỚI huhuh

Answer 1

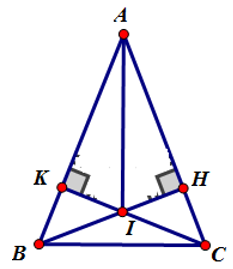
a) Xét ΔAKC và ΔAHB có:

AKC = AHB (= 90^o)

AC = AB (ΔABC cân)

KAH: chung

=> ΔAKC = ΔAHB (g.c.g)

=> AK = AH (2 cạnh tương ứng)

b) Xét ΔAIK và ΔAIH có:

AKI = AHI (= 90^o)

AI: chung

AK = AH (cm câu a)

=> ΔAIK = ΔAIH (ch-cgv)

=> IAK = IAH (2 góc tương ứng)

=> AI là phân giác góc A

c) Gọi giao điểm của AI và BC là O

Xét ΔAOB và ΔAOC có:

AO: chung

OAB = OAC (AO: Phan giác BOC)

AB = AC (ΔABC cân)

=> ΔAOB = ΔAOC (c.g.c) (*)

=> AOB = AOC (2 góc tương ứng)

Mà AOB + AOC = 180^o (kề bù)

=> AOB = AOC = 180^o " 2 = 90^o

=> AI vuông góc BC

d) Từ (*) => OB = OC (2 cạnh tương ứng)

=> AI đi qua trđ BC

Answer 2

a)Xét ΔABH vuông tại H và ΔACK vuông tại K có:

AB = AC (Do ΔABC cân tại A)

góc A chung

=> ΔABH = ΔACK (cạnh huyền – góc nhọn)

⇒ AH = AK (hai cạnh tương ứng).

b) Xét 2 tam giác vuông ΔAKI và ΔAHI ta có:

Cạnh huyền AI chung

Cạnh góc vuông AH = AK (câu a)

=> ΔAKI = ΔAHI (cạnh huyền - cạnh góc vuông)

=> \(\widehat{KAI}=\widehat{HAI}\) (2 góc tương ứng)

=> AI là phân giác của \(\widehat{KAH}\)

Hay: AI là phân giác của \(\widehat{BAC}\)

c) Có: AI là phân giác của \(\widehat{BAC}\)

Hay: AI là đường phân giác của tam giác ABC

Theo tính chất: Trong tam giác cân thì đường phân giác cũng đồng thời là đường cao của tam giác đó.

=> AI cũng là đường cao của tam giác ABC

=> AI ⊥ BC.