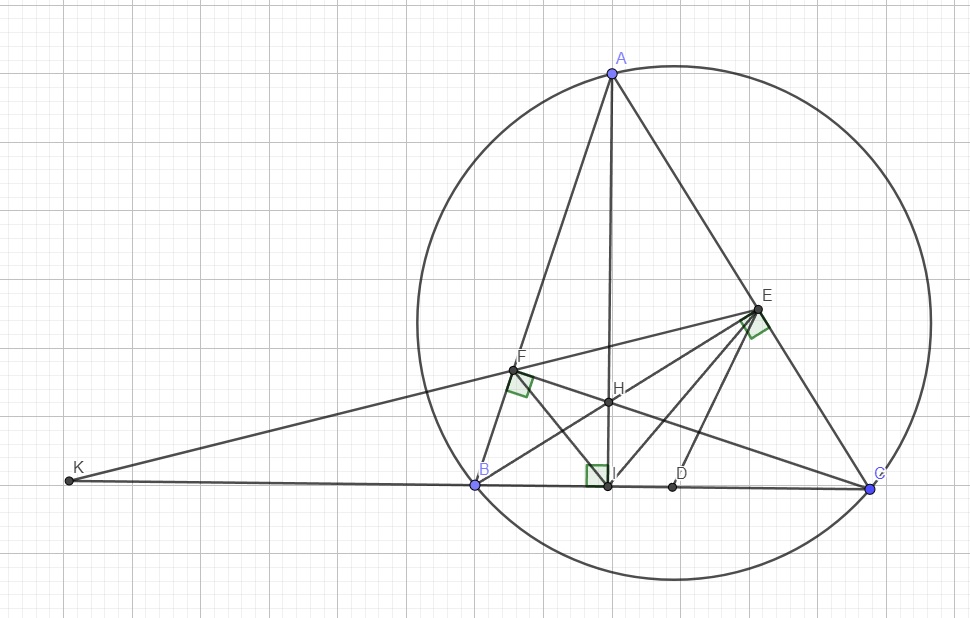
a: Xét tứ giác AFHE có \(\widehat{AFH}+\widehat{AEH}=90^0+90^0=180^0\)
nên AEHF là tứ giác nội tiếp
Xét tứ giác BFEC có \(\widehat{BFC}=\widehat{BEC}=90^0\)
nên BFEC là tứ giác nội tiếp
b: Ta có: BFEC là tứ giác nội tiếp
=>\(\widehat{BFE}+\widehat{BCE}=180^0\)
mà \(\widehat{BFE}+\widehat{KFB}=180^0\)(hai góc kề bù)
nên \(\widehat{KFB}=\widehat{KCE}\)
Xét ΔKFB và ΔKCE có
\(\widehat{KFB}=\widehat{KCE}\)
\(\widehat{FKB}\) chung
Do đó: ΔKFB~ΔKCE
=>\(\dfrac{KF}{KC}=\dfrac{KB}{KE}\)
=>\(KF\cdot KE=KB\cdot KC\)
c.
Do I và F cùng nhìn BH dưới 1 góc vuông nên BFHI nội tiếp
\(\Rightarrow\widehat{FBH}=\widehat{HIF}\) (cùng chắn FH)
E và I cùng nhìn CH dưới 1 góc vuông nên CEHI nội tiếp
\(\Rightarrow\widehat{HCE}=\widehat{HIE}\) (cùng chắn HE)
E và F cùng nhìn BC dưới 1 góc vuông nên BCEF nội tiếp đường tròn đường kính BC
\(\Rightarrow D\) là tâm đường tròn ngoại tiếp (BCEF)
Đồng thời \(\widehat{HCE}=\widehat{FBH}\) (cùng chắn EF) \(\Rightarrow\widehat{HIE}=\widehat{FBH}\)
\(\Rightarrow\widehat{FIE}=\widehat{HIF}+\widehat{HIE}=\widehat{FBH}+\widehat{FBH}=2\widehat{FBH}\)
Trong đường tròn ngoại tiếp BCEF, D là tâm đường tròn nên:
\(\widehat{FDE}=2\widehat{FBE}\) (góc nt và góc ở tâm cùng chắc EF)
Hay \(\widehat{FDE}=2\widehat{FBH}\)
\(\Rightarrow\widehat{FIE}=\widehat{FDE}\)
\(\Rightarrow IDEF\) nội tiếp
\(\Rightarrow\widehat{DIF}+\widehat{KED}=180^0\)
Mà \(\widehat{DIF}+\widehat{KIF}=180^0\) (kề bù)
\(\Rightarrow\widehat{KED}=\widehat{KIF}\)
Lại có góc \(\widehat{IKF}\) chung
\(\Rightarrow\Delta KED\sim\Delta KIF\left(g.g\right)\)
\(\Rightarrow\dfrac{KE}{KI}=\dfrac{KD}{KF}\Rightarrow KE.KF=KI.KD\)
Kết hợp câu b \(\Rightarrow KB.KC=KI.KD\)