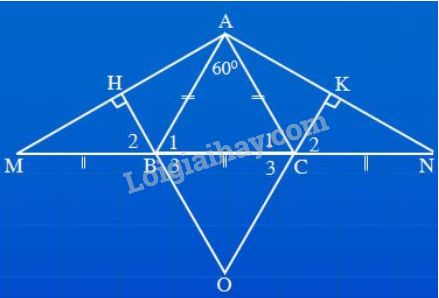
Bài 4: Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối của
tia CB lấy điểm N sao cho BM = CN.
a. Chứng minh rằng tam giác AMN là tam giác cân .
b. Kẻ BH ⊥ AM (H AM), kẻ CK ⊥ AN (K AN).
Chứng minh rằng BH = CK.
c. Chứng minh rằng AH = AK
d. Gọi O là giao điểm của HB và KC. Tam giác OBC là tam giác gì ? Vì sao ?
e. Khi góc BAC = 60độ
và BM = CN = BC, hãy tính số đo các góc của tam giác AMN và xác định dạng của tam giác OBC.
Hình tự vẽ nha
a) Ta có TG ABC cân tại A
suy ra góc ABC = ACB (1)
mà góc ABM kề bù với ABC
và góc ACN kề bù với ACB
suy ra góc ABM = ACN
Xét TG ABM và TG ACN có:
BM = CN (gt)
ABM = ACN (cmt)
AB = AC ( TG ABC cân A)
Do đó TG ABM = TG ACN (c-g-c_
suy ra AM = AN (2 cạnh tương ứng)
⇒ TG AMN cân tại A
b) Xét TG MBH và TG NCK có:
MB = NC (gt)
góc M = N ( TG AMN cân tại A)
góc MHB = NKC = 90o
Do đó TG MBH = TG NCK (ch-gn)
suy ra HM = KN (2 cạnh tương ứng)
c) Ta có: AM = AN (cmt)
mà HM = KN (cmt)
suy ra AH = AK
d) Xét TG AHB và TG AKC có:
AH = AK (cmt)
góc AHB = góc AKC = 90o
AB = AC ( gt)
Do đó TG AHB = TG AKC (ch-cgv)
suy ra góc ABH = ACK (2 góc t/ứ) (2)
Ta có: góc HBO = KCO = 180o (3)
Từ (1) (2) (3) suy ra góc CBO = BCO
suy ra TG BOC cân tại O
phần d dễ rồi bạn tự trả lời nhé
Nhớ tick nha![]()
a/ ΔABC cân tai A
=> \(\widehat{ABC}=\widehat{ACB}\)
Ta có: \(\left\{{}\begin{matrix}\widehat{ABM}+\widehat{ABC}=180^0\\\widehat{ACN}+\widehat{ACB}=180^0\end{matrix}\right.\)
Mà: \(\widehat{ABC}=\widehat{ACB}\) (cmt)
=> \(\widehat{ABM}=\widehat{ACN}\)
Xét ΔABM và ΔACN ta có:
AB = AC (ΔABC cân tại A)
\(\widehat{ABM}=\widehat{ACN}\) (cmt)
MB = CN (GT)
=> ΔABM = ΔACN (c - g - c)
=> \(\widehat{AMB}=\widehat{ANC}\)
Hay: \(\widehat{AMN}=\widehat{ANM}\)
=> ΔAMN cân tại A

d/ Ta có: \(\widehat{HBM}=\widehat{CBO}\) (đối đỉnh)
\(\widehat{KCN}=\widehat{BCO}\) (đối đỉnh)
Mà: \(\widehat{HBM}=\widehat{KCN}\) (đã chứng minh ở câu c)
=> \(\widehat{CBO}=\widehat{BCO}\)
=> ΔBCO cân tai O
Cám ơn mn nhìu lắm nha![]()