a:\(BC=\sqrt{AB^2+AC^2}=25\left(cm\right)\)
\(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{15\cdot20}{25}=12\left(cm\right)\)
Đúng 2
Bình luận (0)
Bài 2: Định lý đảo và hệ quả của định lý Talet
Các câu hỏi tương tự
Bài :cho tam giác ABC vuông tại A, đường cao AH
a) chứng minh tam giác ABC đồng dạng với tam giác HBA
b) chứng minh AH^2 = BH * CH
c) Gọi D và E là hình chiếu của H trên AB và AC. Cho bt BH = 4 cm, CH = 16 cm, hãy tính độ dài DE
d) kẻ trung tuyến AM của tam giác ABC. Tính tỉ số diện tích của tam giác AMH và tam giác ABC khi biết BH = 4cm, CH = 16 cm
Cho tam giác ABC có AB = 18 cm, AC = 12 cm, BC = 9 cm. Trên tia đối của tia CB lấy điểm D sao cho CD = 3 cm. Qua D kẻ đường thẳng song song với AB cắt tia AC tại E. Gọi F là giao điểm của AD và BE. Tính: a) Độ dài CE, DE
Cho tam giác ABC cân tại A. Đường vuông góc với BC tại B cắt đường vuông góc với AC tại C ở D. Vẽ BE vuông góc với CD tại E, gọi M là giao điểm của AD và BE.. Vẽ EN vuông góc BD tại N
a) Chứng minh DE/DM=DC/DA
b) Chứng minh MN//AB
c) Chứng minh ME=MB
Cho DABC vuông tại A, đường phân giác của góc A cắt BC tại D biết AB = 6 cm , AC = 8 cm . a) Tính BC, BD, DC b) Từ trung điểm M của BC kẻ 1 đường thẳng song song với AD cắt cạnh AC tại F và cắt tia đối của tia AB tại E .Chứng minh: . c) Chứng minh: AE = AF
Cho tam giác ABC cân tại A, BC = 8cm, phân giác của góc B cắt đường cáo AH ở K, AK/AH = 3/5 a) Tính độ dài AB b) Đường thẳn vuông góc với BK cắt AH ở E. Tính EH
Cho Tam giác KIM vuông tại K, đường phân giác của góc K cắt IM tại B. a. Tính IM, BI, BM biết KI = 15cm , KM = 20cm . b. Từ trung điểm A của IM kẻ đường thẳng song song với KB cắt cạnh KM tại C và tia IK tại H. Chứng minh: (MA)/(MB) = (AC)/(KB) c. Chứng minh: Tam giác KHC cân và H = MC d. Kẻ các đường phân giác ID và MN của tam giác KIM . Chứng minh : BI/BM * DM/DK * NK/NI =1
Help tui với cần gấp!!!! Cho ∆ABC,đường cao AH trên cạnh AB lấy M sao cho AB=3AM.Qua M kẻ đường thẳng vuông góc với AH tại K cắt AC tại N. 1)CM:AK=1/3 AH 2)CM:AM.AC=AN.AB 3)Cho biết S(ABC) gấp mấy lần S(AMN)? Áp dụng định lí đảo Ta lét và hệ quả của định lí ta lét.
Cho tam giác ABC, điểm D thuộc cạnh BC. Qua D kẻ các đường thẳng song song với AC, AB; chúng
cắt AB, AC tại E, F. Chứng minh tỉ lệ thức:AE/AB+AF/AC=1
Tam giác ABC có đường cao AH. Đường thẳng d song song với BC, cắt các cạnh AB, AC và đường cao AH theo thứ tự tại các điểm B, C và H (h.16)
a) Chứng minh rằng :
dfrac{AH}{AH}dfrac{BC}{BC}
b) Áp dụng : Cho biết AHdfrac{1}{3}AH và diện tích tam giác ABC là 67,5cm^2. Tính diện tích tam giác ABC ?
Đọc tiếp
Tam giác ABC có đường cao AH. Đường thẳng d song song với BC, cắt các cạnh AB, AC và đường cao AH theo thứ tự tại các điểm B', C' và H' (h.16)
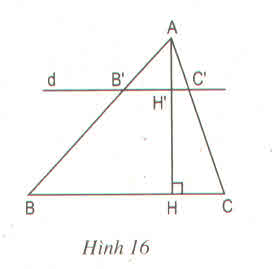
a) Chứng minh rằng :
\(\dfrac{AH'}{AH}=\dfrac{B'C'}{BC}\)
b) Áp dụng : Cho biết \(AH'=\dfrac{1}{3}AH\) và diện tích tam giác ABC là \(67,5cm^2\). Tính diện tích tam giác AB'C' ?