Question

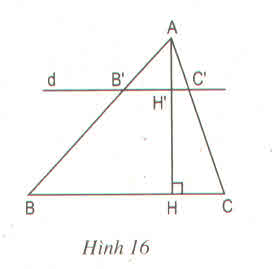
Bài :cho tam giác ABC vuông tại A, đường cao AH

a) chứng minh tam giác ABC đồng dạng với tam giác HBA

b) chứng minh AH^2 = BH * CH

c) Gọi D và E là hình chiếu của H trên AB và AC. Cho bt BH = 4 cm, CH = 16 cm, hãy tính độ dài DE

d) kẻ trung tuyến AM của tam giác ABC. Tính tỉ số diện tích của tam giác AMH và tam giác ABC khi biết BH = 4cm, CH = 16 cm

Answer 1

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có 

\(\widehat{ABC}\) chung

Do đó: ΔABC\(\sim\)ΔHBA

b: XétΔABC vuông tại A có AH là đường cao

nên \(AH^2=BH\cdot CH\)

c: Vì \(AH^2=BH\cdot CH=4\cdot16=64\left(cm\right)\)

nên AH=8cm

Xét tứ giác ADHE có 

\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)

Do đó: ADHE là hình chữ nhật

Suy ra: AH=DE=8(cm)

Answer 2

a, Xét tam giác ABC và tam giác HBA ta có : 

^BAC = ^BHA = 90⁰

^B _ chung 

Vậy tam giác ABC ~ tam giác HBA ( g.g ) 

b, Xét tam giác ABH và tam giác CAH ta có : 

^AHB = ^CHA = 90⁰

^ABH = ^CAH ( cùng phụ ^BAC ) 

Vậy tam giác ABH~ tam giác CAH (g.g )

=> AH/CH=BH/AH => AH^2 = CH.BH 

c, Ta có : AH = 2 . 4 = 8 cm 

Xét tứ giác ADHE có : 

^A = ^ADH = ^AEH = 90⁰ 

Vậy tứ giác ADHE là hcn 

=> AH = DE = 8 cm 

d, Ta có : \(\dfrac{S_{AMH}}{S_{ABC}}=\left(\dfrac{AH}{AC}\right)^2\)

Xét tam giác AHC và tam giác ABC 

^AHC = ^BAC = 90⁰

^HAC = ^B ( cùng phụ ^BAM ) 

Vậy tam giác AHC ~ tam giác BAC ( g.g)

=> AC / BC = HC/AC => AC^2 = HC ( HB + HC ) 

=> AC = 4 . 5 = 20 cm 

Thay vào ta được : \(\left(\dfrac{AH}{AC}\right)^2=\left(\dfrac{8}{20}\right)^2=\dfrac{64}{400}=\dfrac{4}{25}\)