Bài 16:
Ta có: \(A=\dfrac{x^2-6xy+6y^2}{x^2-2xy+y^2}\)
\(=\dfrac{-3x^2+6xy-3y^2+4x^2-12xy+9y^2}{x^2-2xy+y^2}\)
\(=\dfrac{-3\left(x^2-2xy+y^2\right)+\left(4x^2-12xy+9y^2\right)}{x^2-2xy+y^2}\)
\(=\dfrac{-3\left(x^2-2xy+y^2\right)}{x^2-2xy+y^2}+\dfrac{\left(2x\right)^2-2\cdot2x\cdot3y+\left(3y\right)^2}{x^2-2xy+y^2}\)
\(=-3+\dfrac{\left(2x-3y\right)^2}{\left(x-y\right)^2}\)
Ta có: \(\dfrac{\left(2x-3y\right)^2}{\left(x-y\right)^2}\ge0\forall x\ne y\Rightarrow A=-3+\dfrac{\left(2x-3y\right)^2}{\left(x-y\right)^2}\ge-3\)
Dấu "=" xảy ra khi: \(2x-3y=0\Leftrightarrow x=\dfrac{3}{2}y\)
Vậy: \(A_{min}=-3\Leftrightarrow x=\dfrac{3}{2}y\)
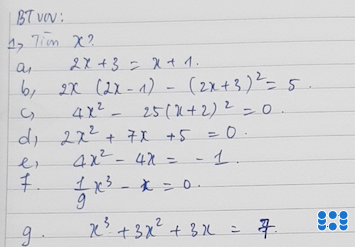
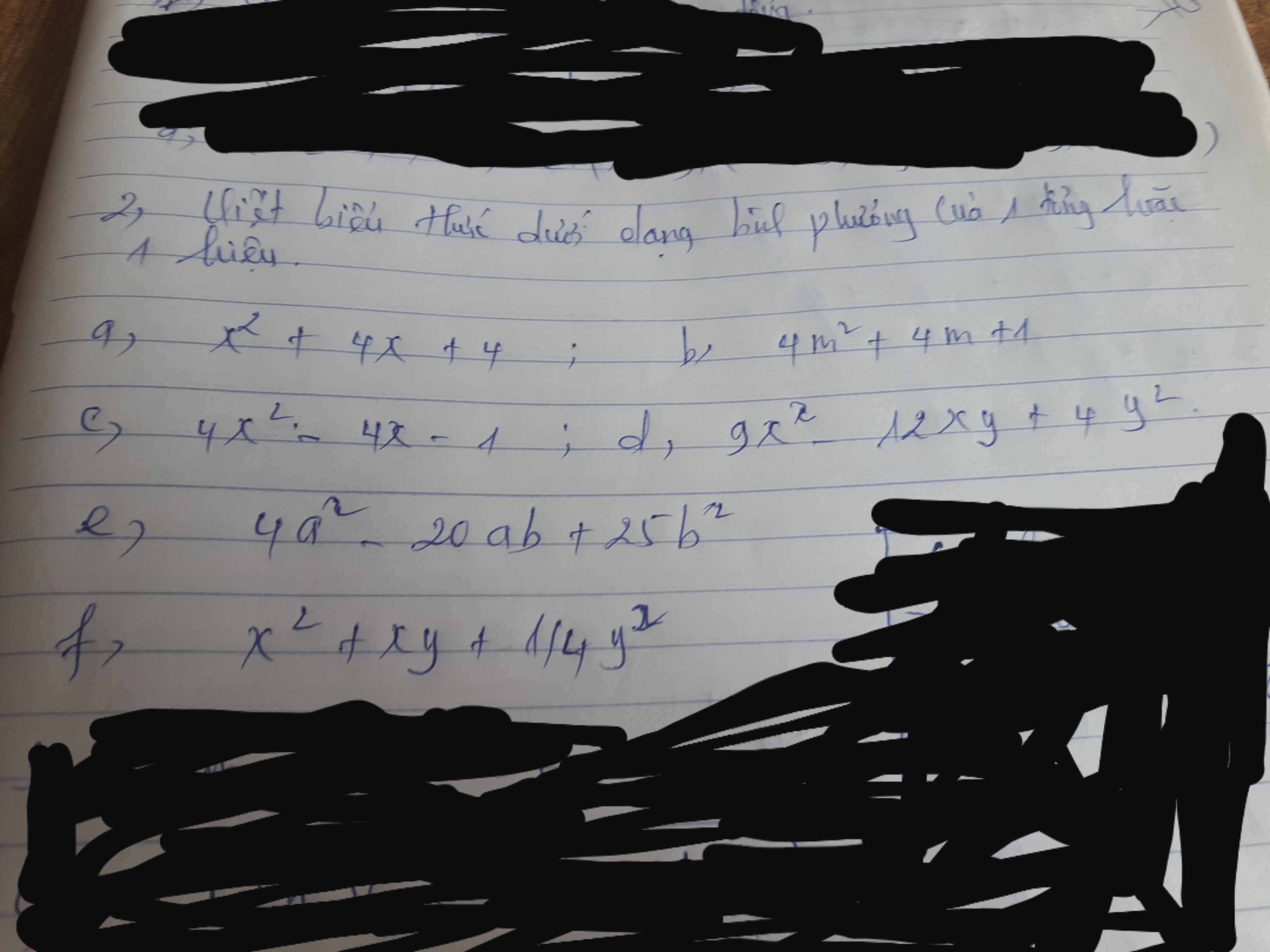
giải thích giùm mình với