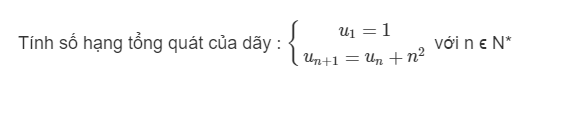Ta có:
\(u_1+u_2+...+u_{2n}=u_1+u_1q+u_1q^2+...+u_1q^{2n-1}\)
\(=u_1\left(1+q+q^2+...+q^{2n-1}\right)\)
\(=\dfrac{u_1\left(q^{2n}-1\right)}{q-1}\)
Lại có:
\(5\left(u_1+u_3+u_5+...+u_{2n-1}\right)\)
\(=5\left(u_1+u_1q^2+u_1q^4+...+u_1q^{2n-2}\right)\)
\(=5u_1\left(1+q^2+q^4+...+q^{2n-2}\right)\)
\(=\dfrac{5u_1\left(q^{2n}-1\right)}{q^2-1}\)
\(\Rightarrow\dfrac{u_1\left(q^{2n}-1\right)}{q-1}=\dfrac{5u_1\left(q^{2n}-1\right)}{q^2-1}\)
\(\Rightarrow q+1=5\)
\(\Rightarrow q=4\)
Đúng 2
Bình luận (0)
