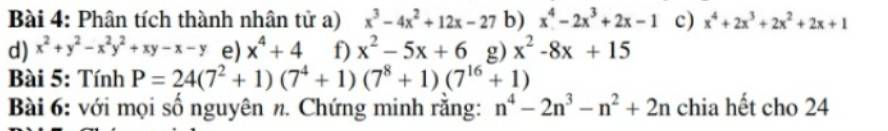Question

Answer 1

6:

A=n^4-2n^3-n^2+2n

=n^3(n-2)-n(n-2)

=(n-2)(n^3-n)

=n(n-1)(n+1)(n-2)

Vì n-2;n-1;n;n+1 là 4 số liên tiếp

nên n(n-1)(n+1)(n-2) chia hết cho 4!=24

5:

\(P=\dfrac{1}{2}\cdot48\left(7^2+1\right)\left(7^4+1\right)\cdot...\cdot\left(7^{16}+1\right)\)

\(=\dfrac{1}{2}\left(7^2-1\right)\left(7^2+1\right)\left(7^4+1\right)\cdot...\cdot\left(7^{16}+1\right)\)

\(=\dfrac{1}{2}\left(7^4-1\right)\left(7^4+1\right)\cdot...\cdot\left(7^{16}+1\right)\)

\(=\dfrac{1}{2}\left(7^8-1\right)\left(7^8+1\right)\left(7^{16}+1\right)\)

\(=\dfrac{1}{2}\left(7^{32}-1\right)\)