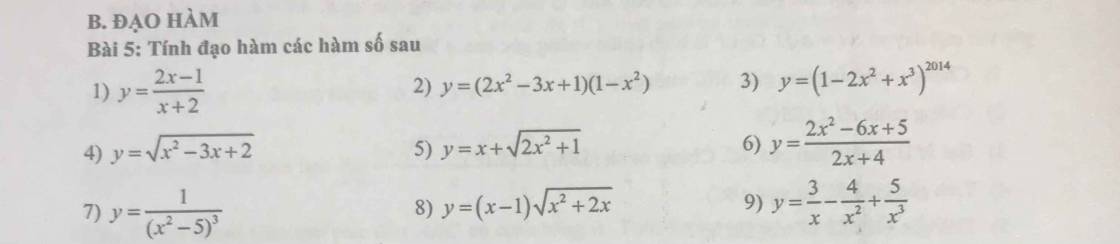1:
\(y'=\dfrac{\left(2x-1\right)'\cdot\left(x+2\right)-\left(2x-1\right)\cdot\left(x+2\right)'}{\left(x+2\right)^2}\)
\(=\dfrac{2x+4-2x+1}{\left(x+2\right)^2}=\dfrac{5}{\left(x+2\right)^2}\)
2:
\(\left(2x^2-3x+1\right)'=2\cdot2x-3=4x-3\)
(1-x^2)'=1-2x
\(y'=\left(4x-3\right)\cdot\left(1-x^2\right)+\left(2x^2-3x+1\right)\left(1-2x\right)\)
\(=4x-4x^3-3+3x^2+2x^2-4x^3-3x+6x^2+1-2x\)
\(=-8x^3+11x^2-x-2\)
5:
\(\sqrt{2x^2+1}'=\dfrac{\left(2x^2+1\right)'}{\sqrt{2x^2+1}}=\dfrac{4x}{\sqrt{2x^2+1}}\)
\(y'=x'+\sqrt{2x^2+1}'=1+\dfrac{4x}{\sqrt{2x^2+1}}\)
Đúng 0
Bình luận (0)
