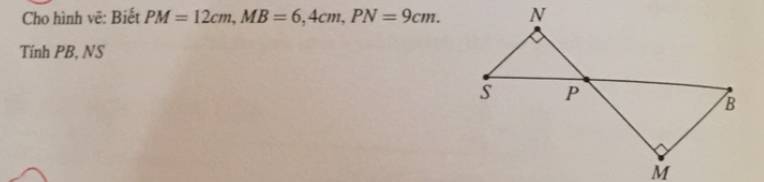Question

Answer 1

\(PB=\sqrt{12^2+6.4^2}=13.6\left(cm\right)\)

Xét ΔNPS vuông tại N và ΔMPB vuông tại M có

góc NPS=góc MPB

DO đó: ΔNPS đồng dạng với ΔMBP

=>NS/MP=PN/BM

=>NS/12=9/6,4

=>NS=16,875(cm)

Answer 2

Lời giải:
$\widehat{M}=\widehat{N}$ (bằng $90^0$). Mà hai góc này ở vị trí so le trong nên $NS\parallel MB$ 

Theo định lý Talet:

$\frac{NS}{MB}=\frac{NP}{PM}=\frac{9}{12}=\frac{3}{4}$

$\Rightarrow NS=MB.\frac{3}{4}=6,4.\frac{3}{4}=4,8$ (cm)

Áp dụng định lý Pitago:

$PB=\sqrt{PM^2+MB^2}=\sqrt{12^2+6,4^2}=13,6$ (cm)