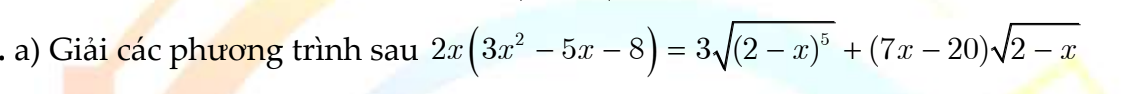\(2x\left(3x^2-5x-8\right)=3\sqrt{\left(2-x\right)^5}+\left(7x-20\right)\sqrt{2-x}\). ĐKXĐ : \(x\le2\)
\(\Leftrightarrow2x\left(3x^2-5x-8\right)=\sqrt{2-x}\left[3\sqrt{\left(2-x\right)^4}+7x-20\right]\)
\(\Leftrightarrow2x\left(3x^2-5x-8\right)=\sqrt{2-x}\left[3\left(2-x\right)^2+7x-20\right]\)
\(\Leftrightarrow2x\left(3x^2-5x-8\right)=\sqrt{2-x}\left(3x^2-5x-8\right)\)
\(\Leftrightarrow2x\left(3x^2-5x-8\right)-\sqrt{2-x}\left(3x^2-5x-8\right)=0\)
\(\Leftrightarrow\left(3x^2-5x-8\right)\left(2x-\sqrt{2-x}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3x^2-5x-8=0\\2x-\sqrt{2-x}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x^2-5x-8=0\\2x=\sqrt{2-x}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x^2-5x-8=0\\4x^2=2-x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x^2-5x-8=0\\4x^2+x-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}x=-1\left(tmđk\right)\\x=\dfrac{8}{3}\left(ktmđk\right)\end{matrix}\right.\\\left[{}\begin{matrix}x=-\dfrac{1-\sqrt{33}}{8}\left(tmđk\right)\\x=-\dfrac{1+\sqrt{33}}{8}\left(tmđk\right)\end{matrix}\right.\end{matrix}\right.\)
Vậy : \(S=\left\{-1;-\dfrac{1+\sqrt{33}}{8};-\dfrac{1-\sqrt{33}}{8}\right\}\)