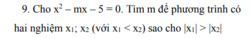Do \(ac=-5< 0\Rightarrow\) phương trình luôn có 2 nghiệm trái dấu
\(\Rightarrow x_1< 0< x_2\Rightarrow\left\{{}\begin{matrix}\left|x_1\right|=-x_1\\\left|x_2\right|=x_2\end{matrix}\right.\)
Theo Viet: \(x_1+x_2=m\)
\(\left|x_1\right|>\left|x_2\right|\Rightarrow-x_1>x_2\)
\(\Rightarrow x_1+x_2< 0\)
\(\Rightarrow m< 0\)
à nhầm xl hén
ta có : \(\Delta=m^2+20>0\), \(\forall m\) nên pt luôn có 2 nghiệm ph/biệt x1 , x2
theo Vi-ét có:
\(\left\{{}\begin{matrix}x_1+x_2=m\\x_1.x_2=-5\end{matrix}\right.\)
Để \(\left|x_1\right|>\left|x_2\right|\) thì \(x_1;x_2\) không là số đối của nhau tức là :\(x_1+x_2\ne0\)
\(\Rightarrow m\ne0\)