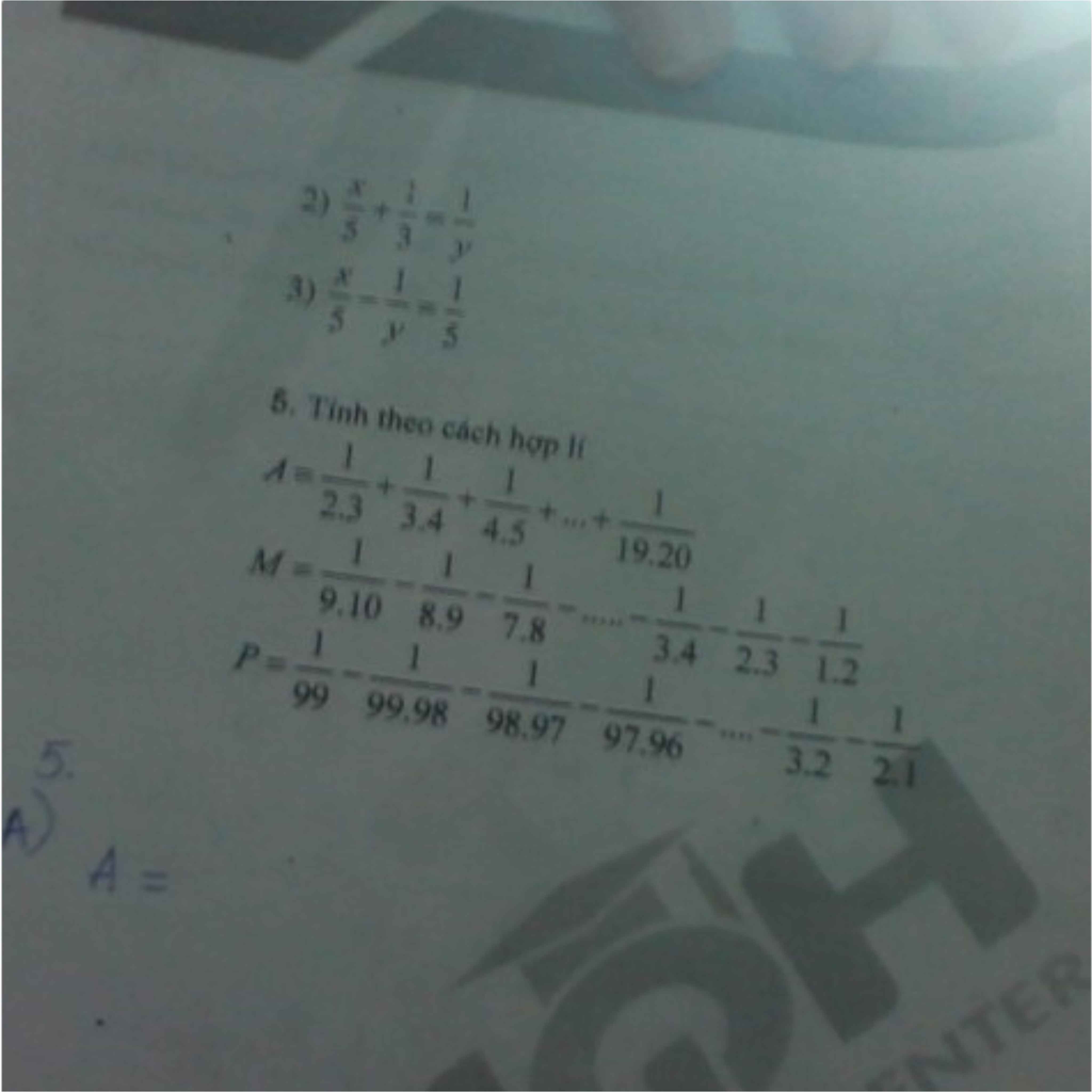Bài 5:
\(A=\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{19.20}\\ =\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{19}-\dfrac{1}{20}\\ =\dfrac{1}{2}-\dfrac{1}{20}\\ =\dfrac{9}{20}\)
A = \(\dfrac{1}{2.3}\)+\(\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{19.20}\)
A= \(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{16}-\dfrac{1}{20}\)
A= \(\dfrac{1}{2}+0+0+...+0-\dfrac{1}{20}\)
A= \(\dfrac{1}{2}-\dfrac{1}{20}\)
A=\(\dfrac{9}{20}\)
GOOD LUCK!!!
Bài 5:
Ta có: \(P=\dfrac{1}{99}-\dfrac{1}{99\cdot98}-\dfrac{1}{98\cdot97}-...-\dfrac{1}{3\cdot2}-\dfrac{1}{2\cdot1}\)
\(=\dfrac{1}{99}-\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{97\cdot98}+\dfrac{1}{98\cdot99}\right)\)
\(=\dfrac{1}{99}-\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{97}-\dfrac{1}{98}+\dfrac{1}{98}-\dfrac{1}{99}\right)\)
\(=\dfrac{1}{99}-1+\dfrac{1}{99}\)
\(=-\dfrac{97}{99}\)