Học tại trường
Chưa có thông tin
Đến từ
Hà Nội , Chưa có thông tin
Số lượng câu hỏi
0
Số lượng câu trả lời
231
Điểm GP
120
Điểm SP
693
Người theo dõi (11)
Đang theo dõi (0)

Câu trả lời:
chữ xấu (thông cảm) ;-;
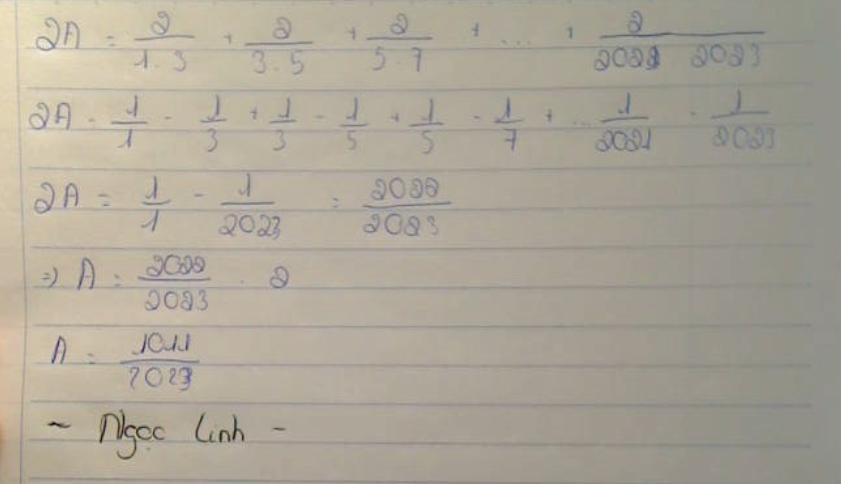

Câu trả lời:
1. need
2. won't be
3. will buy
4. will write
5. will go










