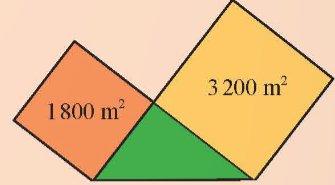
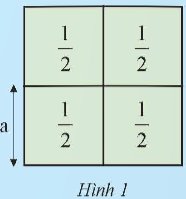
Bốn ô cửa hình vuông diện tích \(\frac{1}{2}{m^2}\) ghép thành cửa sổ Hình 1.
a) Hai bạn An và Mai tính độ dài cạnh a (m) của mỗi ô cửa.
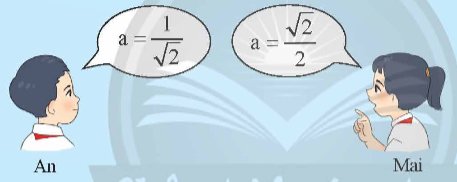
Kết quả của mỗi bạn có đúng không? Giải thích?
b) Biết rằng \(\sqrt 2 \approx 1,4142\). Không dùng máy tính cầm tay, hai bạn tìm giá trị gần đúng của độ dài mỗi ô cửa.
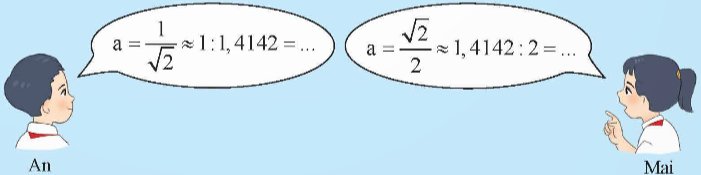
Theo em, bạn nào sẽ tìm ra đáp án nhanh hơn?