Trục căn thức ở mẫu các biểu thức sau:
a) \(\frac{4}{{\sqrt {13} - 3}}\)
b) \(\frac{{10}}{{5 + 2\sqrt 5 }}\)
c) \(\frac{{\sqrt a - \sqrt b }}{{\sqrt a + \sqrt b }}\) với a > 0; b > 0, \(a \ne b\).
Trục căn thức ở mẫu các biểu thức sau:
a) \(\frac{4}{{\sqrt {13} - 3}}\)
b) \(\frac{{10}}{{5 + 2\sqrt 5 }}\)
c) \(\frac{{\sqrt a - \sqrt b }}{{\sqrt a + \sqrt b }}\) với a > 0; b > 0, \(a \ne b\).
Rút gọn các biểu thức sau:
a) \(2\sqrt 3 - \sqrt {27} \)
b) \(\sqrt {45} - \sqrt {20} + \sqrt 5 \)
c) \(\sqrt {64a} - \sqrt {18} - a\sqrt {\frac{9}{a}} + \sqrt {50} \) với a > 0
Thảo luận (1)Hướng dẫn giảia) \(2\sqrt 3 - \sqrt {27} \) \( = 2\sqrt 3 - \sqrt {9.3} \) \( = 2\sqrt 3 - 3\sqrt 3 \) \( = - \sqrt 3 \)
b) \(\sqrt {45} - \sqrt {20} + \sqrt 5 \) \( = \sqrt {5.9} - \sqrt {4.5} + \sqrt 5 \) \( = 3\sqrt 5 - 2\sqrt 5 + \sqrt 5 \) \( = 2\sqrt 5 \)
c) \(\sqrt {64a} - \sqrt {18} - a\sqrt {\frac{9}{a}} + \sqrt {50} \) với a > 0
\(\begin{array}{l} = 8\sqrt a - \sqrt {2.9} - 3\sqrt {\frac{{{a^2}}}{a}} + \sqrt {25.2} \\ = 8\sqrt a - 3\sqrt 2 - 3\sqrt a + 5\sqrt 2 \\ = 5\sqrt a + 2\sqrt 2\end{array}\)
(Trả lời bởi Nguyễn Quốc Đạt)
Tính
a) \(\left( {\sqrt {\frac{4}{3}} + \sqrt 3 } \right)\sqrt 6 \)
b) \(\sqrt {18} :\sqrt 6 + \sqrt 8 .\sqrt {\frac{{27}}{2}} \)
c) \({\left( {1 - 2\sqrt 5 } \right)^2}\)
Thảo luận (1)Hướng dẫn giảia) \(\left( {\sqrt {\frac{4}{3}} + \sqrt 3 } \right)\sqrt 6 = \sqrt {\frac{4}{3}} .\sqrt 6 + \sqrt 3 .\sqrt 6 \) \(= \sqrt {\frac{{24}}{3}} + \sqrt {18} \)\(=\sqrt 8 + \sqrt {18} \)\(= \sqrt {2.4} + \sqrt {2.9} \)\(= 2\sqrt 2 + 3\sqrt 2 \)\(= 5\sqrt 2 \)
b) \(\sqrt {18} :\sqrt 6 + \sqrt 8 .\sqrt {\frac{{27}}{2}} \)\( = \sqrt {\frac{{18}}{6}} + \sqrt {8.\frac{{27}}{2}} \)\( = \sqrt 3 + \sqrt {108} \)\( = \sqrt 3 + \sqrt {36.3} \)\( = \sqrt 3 + 6\sqrt 3 \)\( = 7\sqrt 3 \)
c) \({\left( {1 - 2\sqrt 5 } \right)^2} = 1 - 4\sqrt 5 + 20 = 21 - 4\sqrt 5 \)
(Trả lời bởi Nguyễn Quốc Đạt)
Chứng minh rằng:
a) \(\frac{{a\sqrt b - b\sqrt a }}{{\sqrt {ab} }}:\frac{1}{{\sqrt a + \sqrt b }} = a - b\) với a > 0; b > 0
b) \(\left( {1 + \frac{{a + \sqrt a }}{{\sqrt a + 1}}} \right)\left( {1 - \frac{{a - \sqrt a }}{{\sqrt a - 1}}} \right) = 1 - a\) với a \( \ge \) 0 và a \( \ne \)1
Thảo luận (1)Hướng dẫn giảia) \(\frac{{a\sqrt b - b\sqrt a }}{{\sqrt {ab} }}:\frac{1}{{\sqrt a + \sqrt b }} = a - b\) với a > 0; b > 0
Xét vế trái, ta có:
\(\begin{array}{l}VT = \frac{{a\sqrt b - b\sqrt a }}{{\sqrt {ab} }}:\frac{1}{{\sqrt a + \sqrt b }}\\ = \frac{{\sqrt {ab} \left( {\sqrt a - \sqrt b } \right)}}{{\sqrt {ab} }}.\left( {\sqrt a + \sqrt b } \right)\\ = \left( {\sqrt a - \sqrt b } \right)\left( {\sqrt a + \sqrt b } \right)\\ = a - b = VP\end{array}\)
Vậy \(\frac{{a\sqrt b - b\sqrt a }}{{\sqrt {ab} }}:\frac{1}{{\sqrt a + \sqrt b }} = a - b\)
b) \(\left( {1 + \frac{{a + \sqrt a }}{{\sqrt a + 1}}} \right)\left( {1 - \frac{{a - \sqrt a }}{{\sqrt a - 1}}} \right) = 1 - a\) với a \( \ge \) 0 và a \( \ne \)1
Xét vế trái ta có:
\(\left( {1 + \frac{{a + \sqrt a }}{{\sqrt a + 1}}} \right)\left( {1 - \frac{{a - \sqrt a }}{{\sqrt a - 1}}} \right) = \left( {1 + \frac{{\sqrt a \left( {\sqrt a + 1} \right)}}{{\sqrt a + 1}}} \right)\left( {1 - \frac{{\sqrt a \left( {\sqrt a - 1} \right)}}{{\sqrt a - 1}}} \right)\)
\( = \left( {1 + \sqrt a } \right)\left( {1 - \sqrt a } \right) = 1 - {\left( {\sqrt a } \right)^2} = 1 - a\) = VP.
Vậy \(\left( {1 + \frac{{a + \sqrt a }}{{\sqrt a + 1}}} \right)\left( {1 - \frac{{a - \sqrt a }}{{\sqrt a - 1}}} \right) = 1 - a\)
(Trả lời bởi Nguyễn Quốc Đạt)
Tam giác ABC được vẽ trên ô vuông như Hình 4. Tính diện tích và chu vi của tam giác ABC.
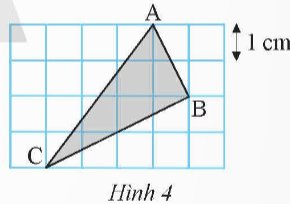
Thảo luận (1)Hướng dẫn giảiTa có:
AB = \(\sqrt{1+2^2} = \sqrt 5\)cm;
BC = \(\sqrt{2^2+4^2} = 2\sqrt 5\)cm;
AC = \(\sqrt{3^2+4^2} = 5\)cm
Chu vi tam giác ABC là: \(\sqrt 5 + 2\sqrt 5 + 5 = 5 + 3 \sqrt5 \)cm
Diện tích tam giác ABC là: \(\frac{1}{2}AB.BC\)= \(\frac{1}{2}.\sqrt 5.2\sqrt 5 = 5\)cm2
(Trả lời bởi Nguyễn Quốc Đạt)
Một vườn hoa gồm ba thửa hình vuông X, Y, Z lần lượt có diện tích như Hình 5. Tính chu vi của vườn hoa đó.
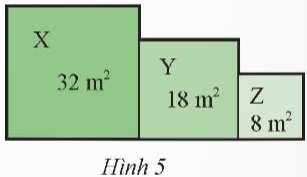
Thảo luận (1)Hướng dẫn giải
Độ dài cạnh hình vuông X là: \(x = \sqrt {32} = 4\sqrt 2 \)m
Độ dài cạnh hình vuông Y là: \(y = \sqrt {18} = 3\sqrt 2 \)m
Ta có cạnh hình vuông Z là: \(z = \sqrt 8 = 2\sqrt 2 \)m
Quan sát hình vẽ ta thấy: AK = BC + DE + FG hay x = BC + DE + FG
Chu vi của vườn hoa là:
\(AB + BC + CD + DE + EF + FG + GH + HI + IK + KA \)
\(= (AB + IK + AK) + (BC + DE + FG) + (CD + HI) + (EF + GH)\)
\(= 3x + x + 2y + 2z\)
\( = 4x + 2y + 2z\)
\( = 4.4\sqrt 2 + 2.3\sqrt 2 + 2.2\sqrt 2 = 26\sqrt 2 (m)\)
Vậy chu vi của vườn hoa đó là: \(26\sqrt 2 \)m.
(Trả lời bởi Nguyễn Quốc Đạt)