Hai bến thuyền A và B nằm sát con đường vuông góc với nhau cách chỗ giao nhau lần lượt là 2 km và 3 km (hình bên). Một ca nô chạy thẳng từ A đến B. Quãng đường ca nô đi được dài bao nhiêu kilômét?

Hai bến thuyền A và B nằm sát con đường vuông góc với nhau cách chỗ giao nhau lần lượt là 2 km và 3 km (hình bên). Một ca nô chạy thẳng từ A đến B. Quãng đường ca nô đi được dài bao nhiêu kilômét?

Cho trục số được vẽ trên lưới ô vuông đơn vị như Hình 1.
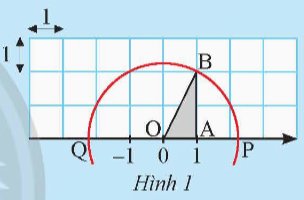
a) Tính độ dài cạnh huyền OB của tam giác vuông OAB.
b) Vẽ đường tròn tâm O bán kính OB, đường tròn này cắt trục số tại hai điểm P và Q.
Gọi x là số thực được biểu diễn bởi P, y là số thực được biểu diễn bởi Q.
Thay mỗi ? bằng số thích hợp để có các đẳng thức:
x2 = ?; y2 = ?.
Thảo luận (1)Hướng dẫn giảia) Áp dụng định lí Pythagore vào tam giác vuông OAB ta có:
OB = \(\sqrt {1 + {2^2}} = \sqrt 5 \)
b) Vì P, Q là hai điểm thuộc đường tròn tâm O bán kính OB nên \(OP = OQ = OB = \sqrt 5 \)
Vì x là số thực được biểu diễn bởi điểm P nên \(x = \sqrt 5 \),
y là số thực được biểu diễn bởi điểm Q nên \(y = -\sqrt 5 \).
Khi đó ta có các đẳng thức:
\({x^2} = {\left( {\sqrt 5 } \right)^2} = 5\)
\({y^2} = {\left( {-\sqrt 5 } \right)^2} = 5\)
(Trả lời bởi Nguyễn Quốc Đạt)
Tìm các căn bậc hai của mỗi số sau:
a) 36; b) \(\dfrac{4}{49}\); c) 1,44; d) 0.
Thảo luận (1)Hướng dẫn giảia) Ta có 62 = 36, nên 36 có hai căn bậc hai là 6 và – 6
b) Ta có \({\left( {\frac{2}{7}} \right)^2}\)= \(\frac{4}{{49}}\), nên \(\frac{4}{{49}}\) có hai căn bậc hai là \(\frac{2}{7}\) và - \(\frac{2}{7}\)
c) Ta có (1,2)2 = 1,44 nên 1,44 có hai căn bậc hai là 1,2 và – 1,2
d) Số 0 chỉ có một căn bậc hai là chính nó \(\sqrt 0 = 0\)
(Trả lời bởi Nguyễn Quốc Đạt)
Sử dụng dấu căn bậc hai để viết các căn bậc hai của mỗi số:
a) 11; b) 2,5; c) −0,09.
Thảo luận (2)Hướng dẫn giảia) Các căn bậc hai của 11 là \(\sqrt {11} \) và - \(\sqrt {11} \)
b) Các căn bậc hai của 2,5 là \(\sqrt {2,5} \) và - \(\sqrt {2,5} \)
c) Do – 0,09 là số âm nên nó không có căn bậc hai.
(Trả lời bởi Nguyễn Quốc Đạt)
Tính:
a) \(\sqrt{1600}\); b) \(\sqrt{0,81}\); c) \(\sqrt{\dfrac{9}{25}}\).
Thảo luận (1)Hướng dẫn giảia) \(\sqrt {1600} = \sqrt {{{40}^2}} = 40\)
b) \(\sqrt {0,81} = \sqrt {{{(0,9)}^2}} = 0,9\)
c) \(\sqrt {\frac{9}{{25}}} = \sqrt {{{\left( {\frac{3}{5}} \right)}^2}} = \frac{3}{5}\)
(Trả lời bởi Nguyễn Quốc Đạt)
Tính giá trị của các biểu thức:
a) \(\left(\sqrt{12}\right)^2\); b) \(\left(-\sqrt{0,36}\right)^2\); c) \(\left(\sqrt{5}\right)^2+\left(-\sqrt{1,21}\right)^2\).
Thảo luận (1)Hướng dẫn giảia) \({\left( {\sqrt {12} } \right)^2} = 12\)
b) \({\left( { - \sqrt {0,36} } \right)^2} = 0,36\)
c) \({\left( {\sqrt 5 } \right)^2} + {\left( { - \sqrt {1,21} } \right)^2} = 5 + 1,21 = 6,21\)
(Trả lời bởi Nguyễn Quốc Đạt)
Biết rằng hình A và hình vuông B trong Hình 2 có diện tích bằng nhau. Tính độ dài cạnh x của hình vuông B.

Thảo luận (1)Hướng dẫn giảiXét hình A:
Ta có diện tích cả hình vuông cạnh 3cm là : 3.3 = 9 cm2
Ta có diện tích cả hình vuông cạnh \(\sqrt 2 \) cm là : \(\sqrt 2 \). \(\sqrt 2 \) = 2 cm2
Suy ra diện tích hình A là: 9 – 2 = 7 cm2
Mà hình vuông B bằng diện tích hình A là 7 cm2
Nên x.x = x2 = 7 suy ra x = \(\sqrt 7 \) cm.
(Trả lời bởi Nguyễn Quốc Đạt)
Sử dụng máy tính cầm tay, tính gần đúng các số sau (kết quả làm tròn đến chữ số thập phân thứ ba):
a) \(\sqrt{11}\); b) \(\sqrt{7,64}\); c) \(\sqrt{\dfrac{2}{3}}\).
Thảo luận (1)Hướng dẫn giảia) \(\sqrt {11} \approx 3,317\)
b) \(\sqrt {7,64} \approx 2,764\)
c) \(\sqrt {\frac{2}{3}} \approx 0,816\)
(Trả lời bởi Nguyễn Quốc Đạt)
Sử dụng máy tính cầm tay để:
a) Tìm các căn bậc hai của 10,08 (kết quả làm tròn đến chữ số thập phân thứ tư).
b) Tính giá trị của biểu thức \(\dfrac{\sqrt{5}-1}{2}\) (kết quả làm tròn đến chữ số thập phân thứ năm).
Thảo luận (1)Hướng dẫn giảia) Ta có hai căn bậc hai của 10,08 là \(\sqrt {10,08} \approx 3,1749\)và \( - \sqrt {10,08} \approx - 3,1749\)
b) \(\frac{{\sqrt 5 - 1}}{2} \approx 0,61803\)
(Trả lời bởi Nguyễn Quốc Đạt)
Một chiếc thang dài 5 m tựa vào bức tường như Hình 3.

a) Nếu chân thang cách chân tường x (m) thì đỉnh thang ở độ cao bao nhiêu so với chân tường?
b) Tính độ cao trên khi x nhận giá trị lần lượt là 1; 2; 3; 4.
Thảo luận (1)Hướng dẫn giảia) Đỉnh thang có độ cao là: \(\sqrt {{5^2} - {x^2}} \) (m).
b) Khi x = 1 thì độ cao là \(\sqrt {{5^2} - {1^2}} = 2\sqrt 6 \) (m)
Khi x = 2 thì độ cao là \(\sqrt {{5^2} - {2^2}} = \sqrt {21} \)(m)
Khi x = 3 thì độ cao là \(\sqrt {{5^2} - {3^2}} = 4\)(m)
Khi x = 4 thì độ cao là \(\sqrt {{5^2} - {4^2}} = 3\)(m)
(Trả lời bởi Nguyễn Quốc Đạt)