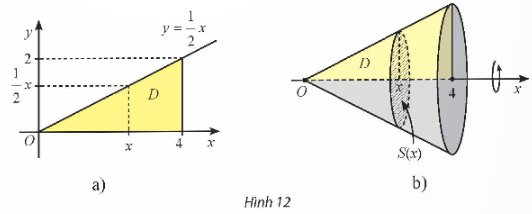
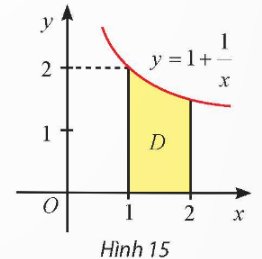
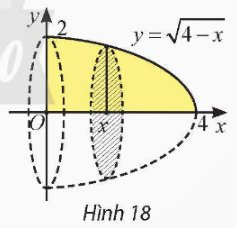
Cho D là hình phẳng giới hạn bởi đồ thị hàm số \(y=f\left(x\right)=\dfrac{1}{2}x\), trục hoành và đường thẳng x = 4 (Hình 12a). Quay hình D xung quanh trục Ox thì được một khối nón, kí hiệu là N (Hình 12b).
a) Cắt khối N bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (0 ≤ x ≤ 4) thì mặt cắt là hình gì? Tính diện tích S(x) của mặt cắt đó.
b) Sử dụng công thức tính thể tích hình khối, tính thể tích của khối nón N.