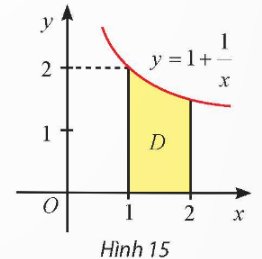
Thể tích khối tròn xoay tạo thành khi quay \(D\) quanh trục \(Ox\) là:
\(V = \pi \int\limits_1^2 {{{\left( {1 + \frac{1}{x}} \right)}^2}dx} = \pi \int\limits_1^2 {\left( {1 + \frac{2}{x} + \frac{1}{{{x^2}}}} \right)dx} = \pi \left. {\left( {x + 2\ln \left| x \right| - \frac{1}{x}} \right)} \right|_1^2 = \pi \left( {\frac{3}{2} + 2\ln 2} \right)\)
Đúng 0
Bình luận (0)