Question

Khi cắt một vật thể hình chiếc nêm bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (−2 ≤ x ≤ 2), mặt cắt là tam giác vuông có một góc 45° và độ dài một cạnh góc vuông là \(\sqrt{4-x^2}\) (dm) (Hình 17). Tính thể tích của vật thể.

Answer 1

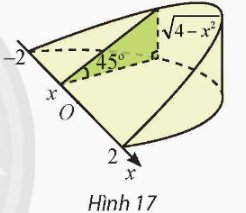
Vì mặt cắt là một tam giác vuông có một góc \({45^o}\), nên mặt cắt là tam giác vuông cân. Do đó diện tích mặt cắt là \(S\left( x \right) = \frac{{{{\left( {\sqrt {4 - {x^2}} } \right)}^2}}}{2} = \frac{{4 - {x^2}}}{2}\).

Thể tích vật thể là:

\(V = \int\limits_{ - 2}^2 {\frac{{4 - {x^2}}}{2}dx}  = \frac{1}{2}\int\limits_{ - 2}^2 {\left( {4 - {x^2}} \right)dx}  = \frac{1}{2}\left. {\left( {4x - \frac{{{x^3}}}{3}} \right)} \right|_{ - 2}^2 = \frac{{16}}{3}\)