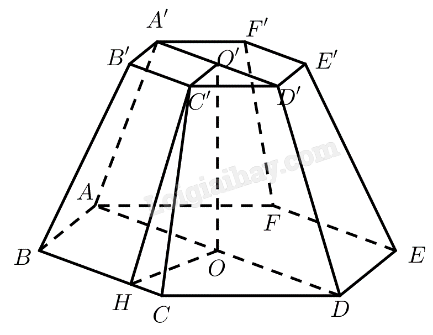
Cho hình lăng trụ lục giác đều \(ABCDEF.A'B'C'D'E'F'\) có cạnh bên bằng \(h\) và cạnh đáy bằng \(a\). Tính \(A'C\) và \(A'D\) theo \(a\) và \(h\).
Bài 3. Hai mặt phẳng vuông góc
Giải mục 4 trang 69, 70, 71 (SGK Chân trời sáng tạo)
Thảo luận (1)
Giải mục 4 trang 69, 70, 71 (SGK Chân trời sáng tạo)
Một chiếc lồng đèn kéo quân có dạng hình lăng trụ lục giác đều với cạnh đáy bằng 10 cm và cạnh bên bằng 30 cm (Hình 20). Tính tổng diện tích các mặt bên của chiếc lồng đèn đó.
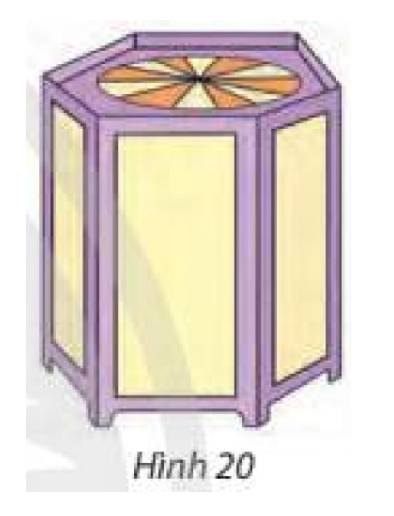
Thảo luận (1)Hướng dẫn giảiDiện tích một mặt bên của lồng đèn là: \(10.30 = 300\left( {c{m^2}} \right)\)
Tổng diện tích các mặt bên của chiếc lồng đèn đó là: \(300.6 = 1800\left( {c{m^2}} \right)\)
(Trả lời bởi Hà Quang Minh)
Giải mục 5 trang 71, 72, 73 (SGK Chân trời sáng tạo)
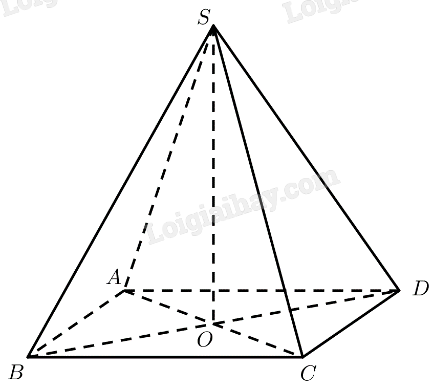
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông với tâm \(O\) và các cạnh bên của hình chóp bằng nhau (Hình 21). Đường thẳng \(SO\) có vuông góc với đáy không?
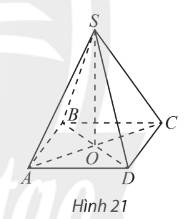
Thảo luận (1)Hướng dẫn giảiTam giác \(SAC\) cân tại \(S \Rightarrow SO \bot AC\)
Tam giác \(SB{\rm{D}}\) cân tại \(S \Rightarrow SO \bot B{\rm{D}}\)
\( \Rightarrow SO \bot \left( {ABCD} \right)\)
(Trả lời bởi Quoc Tran Anh Le)
Giải mục 5 trang 71, 72, 73 (SGK Chân trời sáng tạo)
Cho hình chóp tứ giác đều \(S.ABCD\) có \(O\) là tâm của đáy và \(AB = a,SA = 2a\). Tính \(SO\) theo \(a\).
Thảo luận (1)Hướng dẫn giải\(S.ABCD\) là hình chóp tứ giác đều \( \Rightarrow SO \bot \left( {ABCD} \right)\)
\( \Rightarrow SO \bot AO\)
\(ABC{\rm{D}}\) là hình vuông
\( \Rightarrow AC = AB\sqrt 2 = a\sqrt 2 \Rightarrow AO = \frac{1}{2}AC = \frac{{a\sqrt 2 }}{2}\)
Xét tam giác \(SAO\) vuông tại \(O\) có:
\(SO = \sqrt {S{A^2} - A{O^2}} = \frac{{a\sqrt {14} }}{2}\)
(Trả lời bởi Hà Quang Minh)
Giải mục 5 trang 71, 72, 73 (SGK Chân trời sáng tạo)
Cho biết kim tự tháp Khafre tại Ai Cập có dạng hình chóp tứ giác đều với chiều cao khoảng 136 m và cạnh đáy dài khoảng 152 m. Tính độ dài đường cao của mặt bên xuất phát từ đỉnh của kim tự tháp.
(nguồn: https://vi.wikipedia.org/wiki/ Kim tự tháp_Khafre)

Thảo luận (1)Hướng dẫn giải
Mô hình hoá hình ảnh kim tự tháp bằng hình chóp tứ giác đều \(S.ABC{\rm{D}}\) có \(O\) là tâm của đáy. Kẻ \(SI \bot C{\rm{D}}\left( {I \in C{\rm{D}}} \right)\).
Ta có: \(SO = 136,CD = 152\)
Tam giác \(SCD\) cân tại \(S\)
\( \Rightarrow SI\) vừa là trung tuyến, vừa là đường cao của tam giác
\( \Rightarrow I\) là trung điểm của \(CD\).
Mà \(O\) là trung điểm của \(AD\)
\( \Rightarrow OI\) là đường trung bình của tam giác \(ACD\)
\( \Rightarrow OI = \frac{1}{2}BC = 76\)
\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OI\)
\( \Rightarrow \Delta SOI\) vuông tại \(O\)
\( \Rightarrow SI = \sqrt {S{O^2} + O{I^2}} = 4\sqrt {1517} \approx 155,8\)
Vậy độ dài đường cao của mặt bên xuất phát từ đỉnh của kim tự tháp khoảng 155,8 m.
(Trả lời bởi Quoc Tran Anh Le)
Giải mục 5 trang 71, 72, 73 (SGK Chân trời sáng tạo)
Cho hình chóp đều S.{A_1}{A_2}{A_3}...{A_6}. Mặt phẳng left( P right) song song với mặt đáy và cắt các cạnh bên lần lượt tại {A_1}^prime ,{A_2}^prime ,{A_3}^prime ,...,{A_6}^prime .a) Đa giác {A_1}^prime {A_2}^prime {A_3}^prime ...{A_6}^prime có phải lục giác đều không? Giải thích.b) Gọi O và O lần lượt là tâm của hai lục giác {A_1}{A_2}{A_3}...{A_6} và {A_1}^prime {A_2}^prime {A_3}^prime ...{A_6}^prime . Đường thẳng OO có vuông góc với mặt đáy không?
Đọc tiếp
Cho hình chóp đều \(S.{A_1}{A_2}{A_3}...{A_6}\). Mặt phẳng \(\left( P \right)\) song song với mặt đáy và cắt các cạnh bên lần lượt tại \({A_1}^\prime ,{A_2}^\prime ,{A_3}^\prime ,...,{A_6}^\prime \).
a) Đa giác \({A_1}^\prime {A_2}^\prime {A_3}^\prime ...{A_6}^\prime \) có phải lục giác đều không? Giải thích.
b) Gọi \(O\) và \(O'\) lần lượt là tâm của hai lục giác \({A_1}{A_2}{A_3}...{A_6}\) và \({A_1}^\prime {A_2}^\prime {A_3}^\prime ...{A_6}^\prime \). Đường thẳng \(OO'\) có vuông góc với mặt đáy không?

Thảo luận (1)Hướng dẫn giảia) Ta có:
\(\begin{array}{l}\left( P \right)\parallel \left( {{A_1}{A_2}{A_3}...{A_6}} \right)\\ \Rightarrow {A_1}^\prime {A_2}^\prime \parallel {A_1}{A_2},{A_2}^\prime {A_3}^\prime \parallel {A_2}{A_3},{A_3}^\prime {A_4}^\prime \parallel {A_3}{A_4},{A_4}^\prime {A_5}^\prime \parallel {A_4}{A_5},{A_5}^\prime {A_6}^\prime \parallel {A_5}{A_6},{A_6}^\prime {A_1}^\prime \parallel {A_6}{A_1}\\ \Rightarrow \frac{{{A_1}^\prime {A_2}^\prime }}{{{A_1}{A_2}}} = \frac{{{A_2}^\prime {A_3}^\prime }}{{{A_2}{A_3}}} = \frac{{{A_3}^\prime {A_4}^\prime }}{{{A_3}{A_4}}} = \frac{{{A_4}^\prime {A_5}^\prime }}{{{A_4}{A_5}}} = \frac{{{A_5}^\prime {A_6}^\prime }}{{{A_5}{A_6}}} = \frac{{{A_6}^\prime {A_1}^\prime }}{{{A_6}{A_1}}}\end{array}\)
Mà \({A_1}{A_2} = {A_2}{A_3} = {A_3}{A_4} = {A_4}{A_5} = {A_5}{A_6} = {A_6}{A_1}\)
\( \Rightarrow {A_1}^\prime {A_2}^\prime = {A_2}^\prime {A_3}^\prime = {A_3}^\prime {A_4}^\prime = {A_4}^\prime {A_5}^\prime = {A_5}^\prime {A_6}^\prime = {A_6}^\prime {A_1}^\prime \)
Vậy đa giác \({A_1}^\prime {A_2}^\prime {A_3}^\prime ...{A_6}^\prime \) là lục giác đều.
b) Ta có:
\(\left. \begin{array}{l}O' \in {A_1}^\prime {A_4}^\prime \subset \left( {S{A_1}{A_4}} \right)\\O' \in {A_3}^\prime {A_6}^\prime \subset \left( {S{A_3}{A_6}} \right)\\\left( {S{A_1}{A_4}} \right) \cap \left( {S{A_3}{A_6}} \right) = SO\end{array} \right\} \Rightarrow O' \in SO\)
Mà \(S.{A_1}{A_2}{A_3}...{A_6}\) là hình chóp đều \( \Rightarrow SO \bot \left( {{A_1}{A_2}{A_3}...{A_6}} \right)\)
Vậy \(OO' \bot \left( {{A_1}{A_2}{A_3}...{A_6}} \right)\)
(Trả lời bởi Quoc Tran Anh Le)
Giải mục 5 trang 71, 72, 73 (SGK Chân trời sáng tạo)
Cho hình chóp cụt tam giác đều \(ABC.A'B'C'\) có cạnh đáy lớn \(a\), cạnh đáy nhỏ \(\frac{a}{2}\) và cạnh bên \(2a\). Tính độ dài đường cao của hình chóp cụt đó.
Thảo luận (1)Hướng dẫn giải
Gọi \(O,O'\) lần lượt là tâm của hai đáy \(ABC\) và \(A'B'C'\), \(M,M'\) lần lượt là trung điểm của \(BC\) và \(B'C'\).
Kẻ \(A'H \bot AO\left( {H \in AO} \right) \Rightarrow A'H = OO'\)
\(\Delta ABC\) đều \( \Rightarrow AM = \frac{{a\sqrt 3 }}{2} \Rightarrow AO = \frac{2}{3}AM = \frac{{a\sqrt 3 }}{3}\)
\(\Delta A'B'C'\) đều \( \Rightarrow A'M' = \frac{{\frac{a}{2}.\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{4} \Rightarrow A'O' = \frac{2}{3}A'M' = \frac{{a\sqrt 3 }}{6}\)
\(A'HOO'\) là hình chữ nhật \( \Rightarrow OH = A'O' = \frac{{a\sqrt 3 }}{6}\)
\( \Rightarrow AH = AO - OH = \frac{{a\sqrt 3 }}{6}\)
Tam giác \(AA'H\) vuông tại \(H\)
\( \Rightarrow OO' = A'H = \sqrt {AA{'^2} - A{H^2}} = \frac{{a\sqrt {141} }}{6}\)
(Trả lời bởi Quoc Tran Anh Le)
Giải mục 5 trang 71, 72, 73 (SGK Chân trời sáng tạo)
Một người cần sơn tất cả các mặt của một cái bục để đặt tượng có dạng hình chóp cụt lục giác đều có cạnh đáy lớn 1 m, cạnh bên và cạnh đáy nhỏ bằng 0,7 m. Tính tổng diện tích cần sơn.
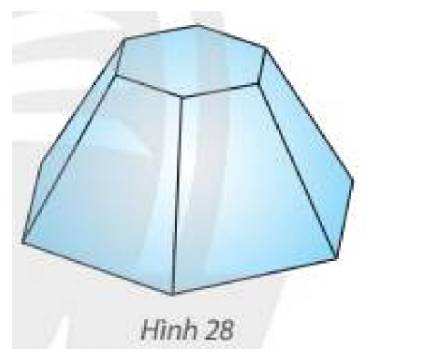
Thảo luận (1)Hướng dẫn giải
Mô hình hoá hình ảnh cái bục bằng hình chóp cụt lục giác đều \(ABC{\rm{DEF}}{\rm{.}}A'B'C'{\rm{D'E'F'}}\) có \(O\) và \(O'\) là tâm của hai đáy. Kẻ \(C'H \bot BC\left( {H \in BC} \right)\).
Ta có: \(BC = 1;CC' = B'C' = 0,7\).
Diện tích đáy lớn là: \(6.\frac{{B{C^2}\sqrt 3 }}{4} = \frac{{3\sqrt 3 }}{2}\)
Diện tích đáy nhỏ là: \(6.\frac{{B'C{'^2}\sqrt 3 }}{4} = \frac{{147\sqrt 3 }}{{200}}\)
\(BCC'B'\) là hình thang cân nên \(HC = \frac{{BC - B'C'}}{2} = 0,15\)
Tam giác \(CC'H\) vuông tại \(H \Rightarrow C'H = \sqrt {CC{'^2} - C{H^2}} = \frac{{\sqrt {187} }}{{20}}\)
Diện tích một mặt bên là: \(\frac{1}{2}\left( {BC + B'C'} \right).C'H = \frac{{17\sqrt {187} }}{{400}}\)
Diện tích sáu mặt bên là: \(6.\frac{{17\sqrt {187} }}{{400}} = \frac{{51\sqrt {187} }}{{200}}\)
Diện tích cần sơn là: \(\frac{{51\sqrt {187} }}{{200}} + \frac{{3\sqrt 3 }}{2} + \frac{{147\sqrt 3 }}{{200}} \approx 7,36\left( {{m^2}} \right)\)
(Trả lời bởi Quoc Tran Anh Le)
Bài 1 trang 73 (SGK Chân trời sáng tạo)
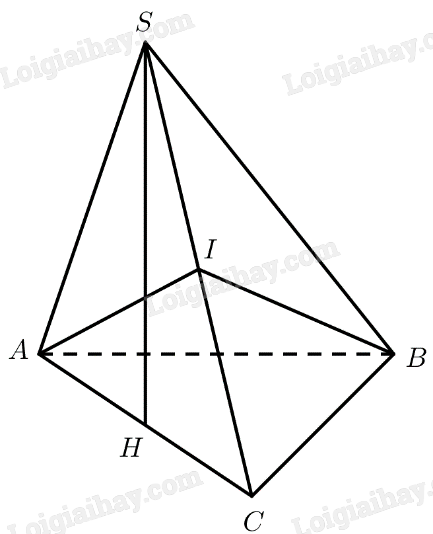
Cho hình chóp \(S.ABC\) có đáy là tam giác vuông tại \(C\), mặt bên \(SAC\) là tam giác đều và nằm trong mặt phẳng vuông góc với \(\left( {ABC} \right)\).
a) Chứng minh rằng \(\left( {SBC} \right) \bot \left( {SAC} \right)\).
b) Gọi \(I\) là trung điểm của \(SC\). Chứng minh rằng \(\left( {ABI} \right) \bot \left( {SBC} \right)\).
Thảo luận (1)Hướng dẫn giải
a) Gọi \(H\) là trung điểm của \(AC\)
\(SAC\) là tam giác đều \( \Rightarrow SH \bot AC\)
Mà \(\left( {SAC} \right) \bot \left( {ABC} \right)\)
\( \Rightarrow SH \bot \left( {ABC} \right) \Rightarrow SH \bot BC\)
Lại có \(AC \bot BC\)
\(\left. \begin{array}{l} \Rightarrow BC \bot \left( {SAC} \right)\\BC \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow \left( {SBC} \right) \bot \left( {SAC} \right)\)
b) \(SAC\) là tam giác đều \( \Rightarrow AI \bot SC\)
\(BC \bot \left( {SAC} \right) \Rightarrow BC \bot AI\)
\(\left. \begin{array}{l} \Rightarrow AI \bot \left( {SBC} \right)\\AI \subset \left( {ABI} \right)\end{array} \right\} \Rightarrow \left( {ABI} \right) \bot \left( {SBC} \right)\)
(Trả lời bởi Quoc Tran Anh Le)
Bài 2 trang 73 (SGK Chân trời sáng tạo)
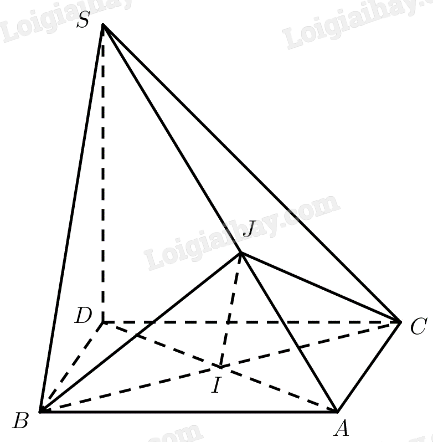
Cho tam giác đều \(ABC\) cạnh \(a\), \(I\) là trung điểm của \(BC\), \(D\) là điểm đối xứng với \(A\) qua \(I\). Vẽ đoạn thẳng \(S{\rm{D}}\) có độ dài bằng \(\frac{{a\sqrt 6 }}{2}\) và vuông góc với \(\left( {ABC} \right)\). Chứng minh rằng:
a) \(\left( {SBC} \right) \bot \left( {SAD} \right)\);
b) \(\left( {SAB} \right) \bot \left( {SAC} \right)\).
Thảo luận (1)Hướng dẫn giải
a) \(ABC{\rm{D}}\) là hình thoi \( \Rightarrow A{\rm{D}} \bot BC\)
\(S{\rm{D}} \bot \left( {ABC} \right) \Rightarrow S{\rm{D}} \bot BC\)
\(\left. \begin{array}{l} \Rightarrow BC \bot \left( {SA{\rm{D}}} \right)\\BC \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow \left( {SBC} \right) \bot \left( {SA{\rm{D}}} \right)\)
b) Kẻ \(IJ \bot SA\left( {J \in SA} \right)\).
\(\Delta ABC\) đều \( \Rightarrow AI = \frac{{a\sqrt 3 }}{2} \Rightarrow A{\rm{D}} = 2AI = a\sqrt 3 \)
\(\Delta SAD\) vuông tại \(D\) \( \Rightarrow S{\rm{A}} = \sqrt {S{D^2} + A{{\rm{D}}^2}} = \frac{{3a\sqrt 2 }}{2}\)
Tam giác \(BCJ\) có \(IJ\) là trung tuyến và \(IJ = \frac{1}{2}BC\)
Vậy tam giác \(BCJ\) vuông tại \(J \Rightarrow BJ \bot JC\)
\(\begin{array}{l}\left. \begin{array}{l}BC \bot \left( {SA{\rm{D}}} \right) \Rightarrow BC \bot SA\\IJ \bot SA\end{array} \right\} \Rightarrow SA \bot \left( {BCJ} \right)\\\left. \begin{array}{l} \Rightarrow SA \bot BJ\\BJ \bot JC\end{array} \right\} \Rightarrow BJ \bot \left( {SAC} \right)\end{array}\)
Mà \(BJ \subset \left( {SAB} \right)\)
Vậy \(\left( {SAB} \right) \bot \left( {SAC} \right)\).
(Trả lời bởi Quoc Tran Anh Le)