Question

Cho hình chóp tứ giác đều \(S.ABCD\) có \(O\) là tâm của đáy và \(AB = a,SA = 2a\). Tính \(SO\) theo \(a\).

Answer 1

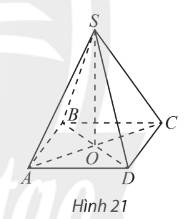
\(S.ABCD\) là hình chóp tứ giác đều \( \Rightarrow SO \bot \left( {ABCD} \right)\)

\( \Rightarrow SO \bot AO\)

\(ABC{\rm{D}}\) là hình vuông

\( \Rightarrow AC = AB\sqrt 2  = a\sqrt 2  \Rightarrow AO = \frac{1}{2}AC = \frac{{a\sqrt 2 }}{2}\)

Xét tam giác \(SAO\) vuông tại \(O\) có:

\(SO = \sqrt {S{A^2} - A{O^2}}  = \frac{{a\sqrt {14} }}{2}\)