Trong Hình 14, MB, MC lần lượt là tiếp tuyến của đường tròn (O) tại B, C; \(\widehat {COB} = {130^o}\). Tính số đo \(\widehat {CMB}\) .
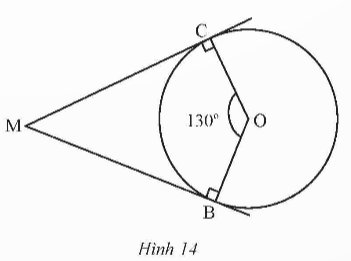
Trong Hình 14, MB, MC lần lượt là tiếp tuyến của đường tròn (O) tại B, C; \(\widehat {COB} = {130^o}\). Tính số đo \(\widehat {CMB}\) .

Quan sát Hình 15. Biết AB, AC lần lượt là tiếp tuyến của đường tròn (O) tại B, C. Tính giá trị của x.
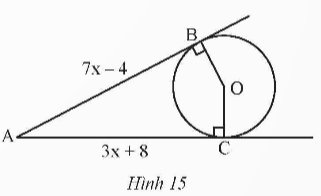
Thảo luận (1)Hướng dẫn giảiVì \(AB,AC\) là tiếp tuyến của \(\left(O\right)\) tại \(B,C\left(gt\right)\)
\(\Rightarrow AB=AC\) (tính chất 2 tiếp tuyến của đường tròn cắt nhau)
\(\Rightarrow7x-4=3x+8\)
\(\Rightarrow4x=12\)
\(\Rightarrow x=3\)
(Trả lời bởi Nguyễn Đức Trí)
Trong Hình 16, AB = 9; BC = 12; AC = 15 và BC là đường kính của đường tròn (O). Chứng minh AB là tiếp tuyến của đường tròn (O).
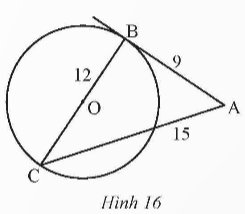
Thảo luận (1)Hướng dẫn giảiTheo hình ta có: AB = 9; BC = 12; AC = 15
Suy ra BC2 = AB2 + AC2 nên tam giác ABC vuông tại B
Hay \(\widehat {CBA} = {90^o}\) suy ra \(AB \bot BC\)
Mà \(O \in BC\) nên \(AB \bot BO\)
Vậy AB đi qua B (B \( \in (O)\)) và \(AB \bot BO = R\) nên AB là tiếp tuyến của đường tròn (O).
(Trả lời bởi Nguyễn Quốc Đạt)
Cho tam giác ABC có đương tròn (O) nằm trong và tiếp xúc với ba cạnh của tam giác. Biết AM = 6 cm; BP = 3 cm; CE = 8 cm (Hình 17). Tính chu vi tam giác ABC.
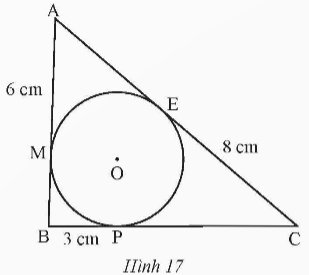
Thảo luận (1)Hướng dẫn giải
Ta có MB và BP là hai tiếp tuyến tại M và P của đường tròn (O) và cắt nhau tại B.
Do đó: BM = BP = 3cm (Tính chất hai tiếp tuyến cắt nhau).
Ta có AM và AE là hai tiếp tuyến tại M và E của đường tròn (O) và cắt nhau tại A.
Do đó: AM = AE = 6cm (Tính chất hai tiếp tuyến cắt nhau).
Ta có CE và CP là hai tiếp tuyến tại E và P của đường tròn (O) và cắt nhau tại C.
Do đó: CE = CP = 8cm (Tính chất hai tiếp tuyến cắt nhau).
Suy ra chu vi tam giác ABC là:
AB + AC + BC = (AM + MB) + (AE + EC) + (BP + PC)
= (6 + 3) + (6 + 8) + (3 + 8) = 34 cm.
(Trả lời bởi Nguyễn Quốc Đạt)
Cho đường tròn (O; R) có đường kính AB. Vẽ dây AC sao cho AC = R. Gọi I là trung điểm dây AC. Đường thẳng OI cắt tiếp tuyến Ax tại M. Chứng minh rằng:
a) \(\widehat {ACB}\) có số đo bằng 90o, từ đó suy ra độ dài của BC theo R;
b) OM là tia phân giác của \(\widehat {COA}\).
c) MC là tiếp tuyến của đường tròn (O; R).
Thảo luận (1)Hướng dẫn giải
a) Theo giả thiết ta có \(\widehat {ACB} = {90^o}\)
Áp dụng định lý Pythagore tam giác ABC vuông tại C, ta có:
AB2 = AC2 + BC2 .Do đó BC2 = AB2 - AC2 = (2R)2 – R2 = 3R2
Mà BC > 0 nên BC = \(R\sqrt 3 \).
b) Ta có IA = IC và AC là dây cung.
Suy ra OI \( \bot \) AC tại I (Trong một đường tròn, đường kính vuông góc với dây thì đi qua trung điểm của dây đó).
Trong tam giác OAC có OA = OC (= R)
Suy ra tam giác OAC là tam giác cân tại O.
Mà OI là đường trung tuyến của tam giác OAC.
Nên OI cũng là đường phân giác của góc COA
Vậy OM là phân giác \(\widehat {COA}\).
c) Xét \(\Delta \)OAM và \(\Delta \)OCM, ta có:
OA = OC = R
\(\widehat {AOM} = \widehat {COM}\) (Vì OM là phân giác góc AOC)
Cạnh chung OM
Suy ra \(\Delta \)OAM = \(\Delta \)OCM (c.g.c)
Nên \(\widehat {OAM} = \widehat {OCM}\) mà \(\widehat {OAM} = {90^o}\)(AM là tiếp tuyến tại A của (O; R))
Nên \(\widehat {OCM} = {90^o}\).
Do đó: \(MC \bot OM\) tại C.
Vậy MC là tiếp tuyến của đường tròn (O; R).
(Trả lời bởi Nguyễn Quốc Đạt)
Cho đường tròn (O; 5 cm) , điểm M nằm ngoài (O) sao cho hai tiếp tuyến MA và MB (A; B là hai tiếp điểm) vuông góc với nhau tại M.
a) Tính độ dài MA và MB.
b) Qua giao điểm I của đoạn thẳng MO và đường tròn (O), vẽ một tiếp tuyến cắt OA, OB lần lượt tại C, D. Tính độ dài CD.
Thảo luận (1)Hướng dẫn giải
a) Xét tứ giác AOBM có:
\(\widehat {MAO} = {90^o}\) (Vì AM là tiếp tuyến của (O))
\(\widehat {OBM} = {90^o}\)(Vì BM là tiếp tuyến của (O))
\(\widehat {AMB} = {90^o}\) (Vì \(AM \bot MB\) tại M).
Do đó, tứ giác AOBM là hình chữ nhật.
Mà OA = OB (= R của (O))
Nên tứ giác AOBM là hình vuông.
Nên ta có MA = MB = OA = 5 cm.
b) Vì AM và MB là hai tiếp tuyến của (O) cắt nhau tại M nên OM là phân giác của
\(\widehat {AOB}\).
Ta có: \(\widehat {AOM} = \frac{1}{2}.\widehat {AOB} = \frac{1}{2}{.90^o} = {45^o}\)
Xét tam giác OCD có OI là đường cao (vì CI là tiếp tuyến của đường trồn tâm O) và OI là đường phân giác .
Do đó: tam giác OCD cân tại O.
Suy ra OI cũng là đường trung tuyến.
Xét tam giác CIO vuông tại I có CI = OI.tan \(\widehat {COI}\) = 5 .tan 45o = 5 cm.
Mà I là trung điểm của CD (Vì OI là trung tuyến tam giác COD).
Do đó CD = 2CI = 2.5 = 10 cm.
(Trả lời bởi Nguyễn Quốc Đạt)
Cho đường tròn (O) , điểm M nằm ngoài (O) sao cho hai tiếp tuyến MA và MB (A; B là hai tiếp điểm) thoả mãn \(\widehat {AMB} = {60^o}\). Biết chu vi tam giác MAB là 18 cm, tính độ dài dây AB.
Thảo luận (1)Hướng dẫn giải
Vì AM, MB là hai tiếp tuyến suy ra \(MA \bot AO;MB \bot BO\).
Xét tam giác vuông AMO và tam giác vuông BMO có:
MO là cạnh chung
OA = OB
Suy ra \(\Delta \)AMO = \(\Delta \)BMO (cạnh huyền – cạnh góc vuông)
Nên MA = MB. Do đó tam giác MAB cân tại M.
Mặt khác, ta có: \(\widehat {AMB} = {60^o}\) nên tam giác MAB đều suy ra AB = MA = MB
Mà AB + AM + MB = \({P_{MAB}}\) = 18
Suy ra 3AB = 18 nên AB = 6 cm.
(Trả lời bởi Nguyễn Quốc Đạt)
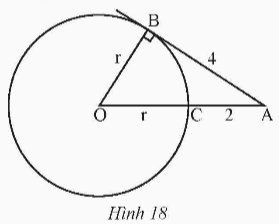
Trong Hình 18, AB là tiếp tuyến của đường tròn (O) tại B.
a) Tính bán kính r của đường tròn (O).
b) Tính chiều dài cạnh OA của tam giác ABO.
Thảo luận (1)Hướng dẫn giảia) Ta có AB là tiếp tuyến của đường tròn (O) tại B. Do đó \(AB \bot OB\).
Ta có: OA = OC + CA = r + 2
Xét tam giác OAB vuông tại B, ta có:
OA2 = OB2 + AB2 (Áp dụng định lý Pythagore)
Suy ra \({(r + 2)^2} = {r^2} + {4^2}\)
\({r^2} + 4r + 4 = {r^2} + 16\)
4r = 12
r = 3 .
b) Xét tam giác OAB vuông tại B, ta có:
OA2 = OB2 + AB2 = 32 + 42 = 52.
Suy ra OA = 5.
(Trả lời bởi Nguyễn Quốc Đạt)