Tìm đạo hàm của mỗi hàm số sau:
a) \(y = 4{x^3} - 3{x^2} + 2x + 10\)
b) \(y = \frac{{x + 1}}{{x - 1}}\)
c) \(y = - 2x\sqrt x \)
d) \(y = 3\sin x + 4\cos x - \tan x\)
e) \(y = {4^x} + 2{e^x}\)
f) \(y = x\ln x\)
Tìm đạo hàm của mỗi hàm số sau:
a) \(y = 4{x^3} - 3{x^2} + 2x + 10\)
b) \(y = \frac{{x + 1}}{{x - 1}}\)
c) \(y = - 2x\sqrt x \)
d) \(y = 3\sin x + 4\cos x - \tan x\)
e) \(y = {4^x} + 2{e^x}\)
f) \(y = x\ln x\)
Cho hàm số \(f(x) = {2^{3x + 2}}\)
a) Hàm số f(x) là hàm hợp của hàm số nào?
b) Tìm đạo hàm của f(x)
Thảo luận (1)Hướng dẫn giảia) Hàm số f(x) là hàm hợp của hàm số \(y = {a^x}\)
b) \(f'(x) = \left( {{2^{3x + 2}}} \right)' = \left( {3x + 2} \right)'{.2^{3x + 2}}.\ln 2 = {3.2^{3x + 2}}.\ln 2\)
(Trả lời bởi Quoc Tran Anh Le)
Tìm đạo hàm của mỗi hàm số sau:
a) \(y = \sin 3x + {\sin ^2}x\)
b) \(y = {\log _2}(2x + 1) + {3^{ - 2x + 1}}\)
Thảo luận (1)Hướng dẫn giảia: \(y'=\left(sin3x\right)'+\left(sin^2x\right)'=3\cdot cos3x+sin\left(x+pi\right)\)
b: \(y'=\left(log_2\left(2x+1\right)\right)'+\left(3^{-2x+1}\right)'\)
\(=\dfrac{2}{\left(2n+1\right)\cdot ln2}-2\cdot3^{-2x+1}\cdot ln3\)
(Trả lời bởi Nguyễn Lê Phước Thịnh)
Viết phương trình tiếp tuyến của đồ thị hàm số sau:
a) \(y = {x^3} - 3{x^2} + 4\) tại điểm có hoành độ \({x_0} = 2\)
b) \(y = \ln x\) tại điểm có hoành độ \({x_0} = e\)
c) \(y = {e^x}\) tại điểm có hoành độ \({x_0} = 0\)
Thảo luận (1)Hướng dẫn giảia) \(y' = \left( {{x^3} - 3{x^2} + 4} \right)' = 3{x^2} - 6x\), \(y'\left( 2 \right) = {3.2^2} - 6.2 = 0\)
Thay \({x_0} = 2\) vào phương trình \(y = {x^3} - 3{x^2} + 4\) ta được: \(y = {2^3} - {3.2^2} + 4 = 0\)
Ta có phương trình tiếp tuyến của đồ thị hàm số: \(y = 0.(x - 2) + 0 = 0\)
Vậy phương trình tiếp tuyến của đồ thị hàm số là y = 0
b) \(y' = \left( {\ln x} \right)' = \frac{1}{x}\), \(y'(e) = \frac{1}{e}\)
Thay \({x_0} = e\) vào phương trình \(y = \ln x\) ta được: \(y = \ln e = 1\)
Ta có phương trình tiếp tuyến của đồ thị hàm số: \(y = \frac{1}{e}.\left( {x - e} \right) + 1 = \frac{1}{e}x - 1 + 1 = \frac{1}{e}x\)
Vậy phương trình tiếp tuyến của đồ thị hàm số là: \(y = \frac{1}{e}x\)
c) \(y' = \left( {{e^x}} \right)' = {e^x},\,\,y'(0) = {e^0} = 1\)
Thay \({x_0} = 0\) vào phương trình \(y = {e^x}\) ta được: \(y = {e^0} = 1\)
Ta có phương trình tiếp tuyến của đồ thị hàm số: \(y = 1.\left( {x - 0} \right) + 1 = x + 1\)
Vậy phương trình tiếp tuyến của đồ thị hàm số là: \(y = x + 1\)
(Trả lời bởi Quoc Tran Anh Le)
Một viên đạn được bắn lên từ mặt đất theo phương thẳng đứng với tốc độ ban đầu \({v_0} = 196m/s\) (bỏ qua sức cản của không khí). Tìm thời điểm tại đó tốc độ của viên đạn bằng 0. (lấy \(g = 9,8m/{s^2}\))
Thảo luận (1)Hướng dẫn giảiCho Ox theo phương thẳng đứng, chiều hướng từ mặt đất lên trời, gốc O là vị trí viên đạn được bắn lên, khi đó phương trình chuyển động của viên đạn là: \(y = {v_0}t - \frac{1}{2}g{t^2}\,\,\left( {g = 9,8m/{s^2}} \right)\)
Ta có vận tốc tại thời điểm t là: \(v = y'\left( t \right) = {v_0} - gt\)
Do đó: \(v = 0 \Rightarrow {v_0} - gt = 0 \Leftrightarrow t = \frac{{{v_0}}}{g} = \frac{{196}}{{9.8}} = 20\,\,(s)\)
(Trả lời bởi Hà Quang Minh)
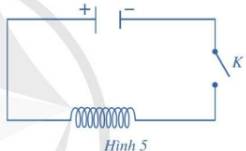
Cho mạch điện như Hình 5. Lúc đầu tụ điện có điện tích \({Q_0}\). Khi đóng khóa K, tụ điện phóng điện qua cuộn dây; điện tích q của tụ điện phụ thuộc vào thời gian t theo công thức \(q(t) = {Q_0}\sin \omega t\), trong đó \(\omega \) là tốc độ góc. Biết rằng cường độ I(t) của dòng diện tại thời điểm t được tính theo công thức \(I(t) = q'(t)\). Cho biết \({Q_0} = {10^{ - 8}}(C)\) và \(\omega = {10^6}\pi \,\,\,(rad/s)\). Tính cường độ của dòng điện tại thời điểm \(t = 6(s)\) (tính chính xác đến \({10^{ - 5}}(mA)\)
Thảo luận (1)Hướng dẫn giảiCông thức tổng quát của cường độ dòng điện tại thời gian t là:
\(I\left(t\right)=q'\left(t\right)=Q_0\cdot\omega\cdot cos\left(\omega t\right)\)
=>\(I\left(6\right)=10^{-8}\cdot10^6\cdot\pi\cdot cos\left(10^6\cdot pi\cdot6\right)=0.01\pi\left(A\right)\)
(Trả lời bởi Nguyễn Lê Phước Thịnh)