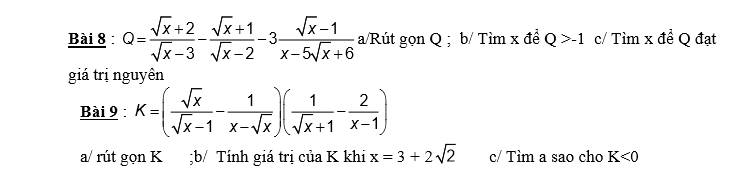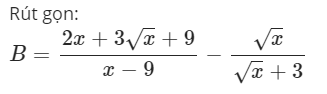Bài 8:
a: \(Q=\dfrac{x-4-x+2\sqrt{x}+3-3\sqrt{x}+3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{-\sqrt{x}+2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}=\dfrac{-1}{\sqrt{x}-3}\)
b: Q>-1
=>Q+1>0
=>\(\dfrac{\sqrt{x}-3-1}{\sqrt{x}-3}>0\)
=>(căn x-4)/(căn x-3)>0
=>căn x-4>0 hoặc căn x-3<0
=>0<x<9 hoặc x>16
c: Q nguyên
=>căn x-3 thuộc {1;-1}
=>x=16
9:
a: \(K=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}-1-2}{x-1}\)
\(=\dfrac{\sqrt{x}-3}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
b: Khi x=3+2căn 2 thì \(K=\dfrac{\sqrt{2}+1-3}{\left(\sqrt{2}+1\right)\cdot\sqrt{2}}=\dfrac{\sqrt{2}-2}{\sqrt{2}\left(\sqrt{2}+1\right)}=-3+2\sqrt{2}\)
c: K<0
=>(căn x-3)/(căn x-1)<0
=>1<x<9