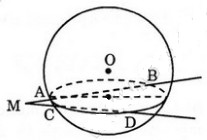
a) Gọi (P) là mặt phẳng chứa hai đường thẳng đã cho. Mặt phẳng (P) cắt mặt cầu S(O;r) theo một đường tròn tâm I, là hình chiếu vuông góc của O lên mặt phẳng (P).
Xét hai tam giác MAD và MCB có góc 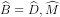 chung nên hai tam giác đó đồng dạng.
chung nên hai tam giác đó đồng dạng.
Vì vậy: 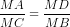 => MA.MB = MC.MD.
=> MA.MB = MC.MD.
b) Đặt MO = d, ta có Oi vuông góc với (P) và ta có:
MO2= MI2 = OI2 và OA2 = OI2 + IA2
Hạ IH vuông góc AB, ta có H là trung điểm của AB.
Ta có MA = MH - HA; MB = MH + HB = MH + HA.
Nên MA.MB =
MH2 – HA2 = (MH2 + HI2) – (HA2 + IH2)
= MI2 – IA2 = ( MI2 + OI2) – (IA2 + OI2)
= MO2 – OẢ2
= d2 – r2
Vậy MA.MB = d2 – r2




