Bài 4: Góc tạo bởi tiếp tuyến và dây cung
Các câu hỏi tương tự
1/ Từ điểm M nằm ngoài đường tròn (O), kẻ các tiếp tuyến MB, MD và 1 cát tuyến MAC ( A nằm giữa M và C ). Chứng minh: a/ MD2 = MA. MC b/ AB.CD = AD.BC
Cho đường tròn (O;R=6cm). Lấy điểm M sao cho OM= 10cm. Kẻ tiếp tuyến MA và MB a. Tính MA, MB b. Kẻ các tuyến MCD. Tính tích MC.MD c. Gọi H là giao điểm của đoạn thẳng MO và AB. Chứng minh rằng: MC.MD=MH.MO d. Gọi E là giao điểm của đoạn thẳng với đường tròn O. Chứng minh rằng: góc EDB =1/2 góc MAB
Cho đường tròn (O) và điểm M nằm bên ngoài đường tròn đó. Qua điểm M kẻ tiếp tuyến MT và cát tuyến MAB.
Chứng minh MT2 = MA. MB.
Từ một điểm M ở ngoài đường tròn (O), vẽ hai tiếp tuyến MA,MB đến đường tròn ( A,B là hai tiếp điểm). Qua À vẽ đường thẳng song song với MV, cắt đường tròn tại E, đoạn thẳng ME cắt đường tròn tại F. Hai đường thẳng AF và MB cắt nhau tại I. CHỨNG MINH : 1) Tứ giác MAOB nội tiếp đường tròn 2) IB mủ 2 = IF.IA
Từ điểm M nằm bên ngoài (O), vẽ hai tiếp tuyến MA, MB và cát tuyến MCD với (O). Gọi I là giao điểm của AB và CD. Cm \(\dfrac{IC}{ID}=\dfrac{MC}{MD}\)
Từ một điểm M cố định ở bên ngoài đường tròn (O) ta kẻ một tiếp tuyến MT và một cát tuyến MAB của đường tròn đó.
a) Chứng minh rằng ta luôn có MT^2MA.MB và tích này không phụ thuộc vị trí của cát tuyến MAB
b) Ở hình 2, khi cho MT 20 cm, MB 50 cm, tính bán kính đường tròn ?
Đọc tiếp
Từ một điểm M cố định ở bên ngoài đường tròn (O) ta kẻ một tiếp tuyến MT và một cát tuyến MAB của đường tròn đó.
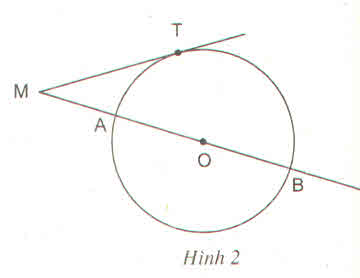
a) Chứng minh rằng ta luôn có \(MT^2=MA.MB\) và tích này không phụ thuộc vị trí của cát tuyến MAB
b) Ở hình 2, khi cho MT = 20 cm, MB = 50 cm, tính bán kính đường tròn ?
từ M nằm ngoài đường tròn tâm O vẽ 2 tiếp tuyến MA và MB và các tuyến MCD thuộc đường tròn, gọi I là giao điểm AB và CD. CMR: IC/ID=MC/MD
Từ điểm A ở ngoài đường tròn (O) vẽ 2 tiếp tuyến AB, AC và cát tuyến AMN của đường tròn đó. Gọi I là trung điểm của dây MN.
a) Chứng minh: Năm điểm A, B, I, O, C cùng nằm trên một đường tròn, xác định tâm và bán kính của đường tròn này.
b) Vẽ đường kính BD. Chứng minh CD song song với OA.
Cho đường tròn tâm (O) điểm A nằm ngoài đường tròn vẽ tiếp tuyến AB và cát tuyến ACD Chứng minh AB^2=AC.AD









