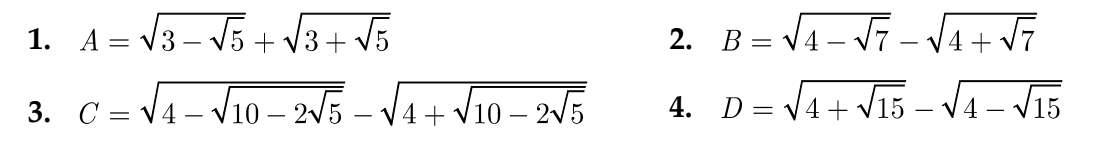1. \(A=\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{5}}\)
\(\Rightarrow A^2=3-\sqrt{5}+2\sqrt{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}+3+\sqrt{5}\)
\(=6+2\sqrt{4}=10\)
\(\Rightarrow A=\sqrt{10}\)
2. \(B=\sqrt{4-\sqrt{7}}-\sqrt{4+\sqrt{7}}\)
\(\Rightarrow B\sqrt{2}=\sqrt{8-2\sqrt{7}}-\sqrt{8+2\sqrt{7}}\)
\(=\sqrt{\left(1-\sqrt{7}\right)^2}-\sqrt{\left(1+\sqrt{7}\right)^2}\)
\(=\sqrt{7}-1-1-\sqrt{7}=-2\)
\(\Rightarrow B=-\dfrac{2}{\sqrt{2}}=-\sqrt{2}\)
3. \(C=\sqrt{4-\sqrt{10-2\sqrt{5}}}-\sqrt{4+\sqrt{10-2\sqrt{5}}}\)
\(\Rightarrow-C=\sqrt{4+\sqrt{10-2\sqrt{5}}}-\sqrt{4-\sqrt{10-2\sqrt{5}}}\)
\(\Rightarrow-C^2=4+\sqrt{10-2\sqrt{5}}-2\sqrt{\left(4+\sqrt{10-2\sqrt{5}}\right)\left(4-\sqrt{10-2\sqrt{5}}\right)}+4-\sqrt{10-2\sqrt{5}}\)
\(=8-2\sqrt{16-10+2\sqrt{5}}\)
\(=8-2\sqrt{6+2\sqrt{5}}\)
\(=8-2\sqrt{\left(1+\sqrt{5}\right)^2}\)
\(=8-2\left(1+\sqrt{5}\right)=6-2\sqrt{5}=\left(1-\sqrt{5}\right)^2\)
\(\Rightarrow-C=\sqrt{\left(1-\sqrt{5}\right)^2}=\sqrt{5}-1\)
\(\Rightarrow C=1-\sqrt{5}\)
4. \(D=\sqrt{4+\sqrt{15}}-\sqrt{4-\sqrt{15}}\)
\(\Rightarrow D^2=4+\sqrt{15}-2\sqrt{\left(4+\sqrt{15}\right)\left(4-\sqrt{15}\right)}+4-\sqrt{15}\)
\(=8-2\sqrt{16-15}=6\)
\(\Rightarrow D=\sqrt{6}\)