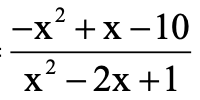\(E=6a+3-9a^2\)
\(=-\left(9a^2-6a-3\right)\)
\(=-\left(\left(3a\right)^2-2.3a+1-4\right)\)
\(=-\left(3a-1\right)^2+4\)
Vì \(-\left(3a-1\right)^2\le0\forall a\)
\(\Rightarrow E\le4\forall x\)
\(MaxE=4\Leftrightarrow x=\dfrac{1}{3}\)
\(e=6a+3-9a^2\)
\(=-9a^2+6a-1+4\)
\(=-\left(9a^2-6a+1\right)+4\)
\(=-\left[\left(3a\right)^2-2\cdot3a\cdot1+1^2\right]+4\)
\(=-\left(3a-1\right)^2+4\)
Ta thấy: \(\left(3a-1\right)^2\ge0\forall a\)
\(\Rightarrow-\left(3a-1\right)^2\le0\forall a\)
\(\Rightarrow-\left(3a-1\right)^2+4\le4\forall a\)
Dấu \("="\) xảy ra \(\Leftrightarrow3a-1=0\Leftrightarrow a=\dfrac{1}{3}\)
Vậy \(e_{max}=4\) khi \(a=\dfrac{1}{3}.\)
#\(Toru\)