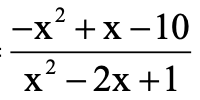Đặt \(x-1=t\Rightarrow x=t+1\)
\(A=\dfrac{-\left(t+1\right)^2+t+1-10}{t^2}=\dfrac{-t^2-t-10}{t^2}=-\dfrac{10}{t^2}-\dfrac{1}{t}-1=-\dfrac{1}{10}\left(\dfrac{1}{t}-\dfrac{1}{20}\right)^2-\dfrac{39}{40}\ge-\dfrac{39}{40}\)
\(A_{min}=-\dfrac{39}{40}\) khi \(\dfrac{1}{t}=\dfrac{1}{20}\Rightarrow x=21\)