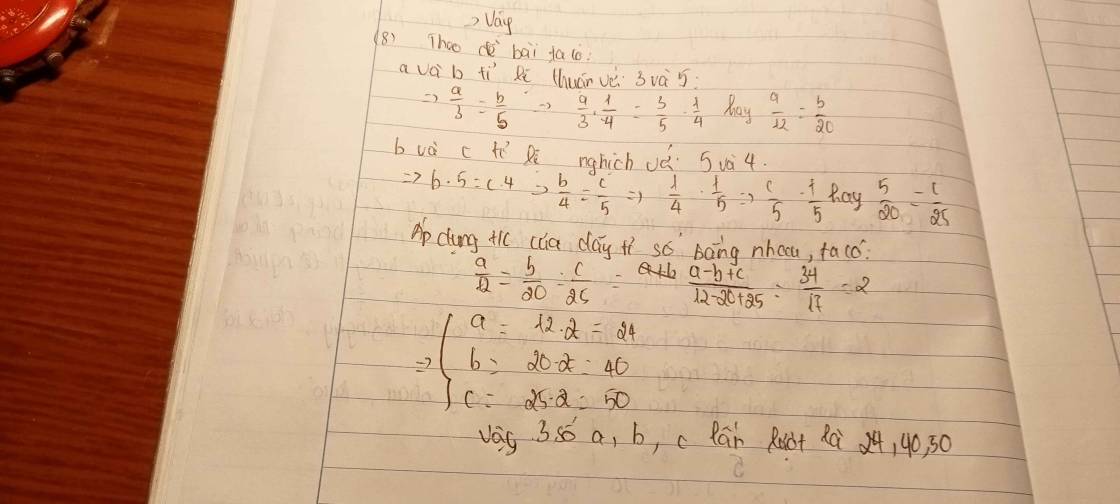Giải :
Theo đề bài ta có :
a và b tỉ lệ thuận với 3 và 5 : \(\frac{a}{3}=\frac{b}{5}\)(1)
b và c tỉ lệ ngịch với 5 và 4 : \(\frac{b}{\frac{1}{5}}=\frac{c}{\frac{1}{4}}\)(2)
=> \(\frac{b}{5}=\frac{c}{\frac{25}{4}}\)
Từ ( 1 ) và ( 2 ) => \(\frac{a}{3}=\frac{b}{5}=\frac{c}{\frac{25}{4}}\)
Theo t/c của dãy tỉ số bằng nhau ta có :
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{\frac{25}{4}}=\frac{a-b+c}{3-5+\frac{25}{4}}=\frac{34}{\frac{17}{4}}=8\)
\(\frac{a}{3}=8\Rightarrow a=8.3=24\)
\(\frac{b}{5}=8\Rightarrow b=8.5=40\)
\(\frac{c}{\frac{25}{4}}8\Rightarrow c=8.\frac{25}{4}=50\)
![]()
Theo bài ta có:
a và b tỉ lệ thuận với 3 và 5 : \(\frac{a}{3}\) = \(\frac{b}{5}\) (1)
b và c tỉ lệ nghịch với 5 và 4 : \(\frac{b}{\frac{1}{5}}\) = \(\frac{c}{\frac{1}{4}}\) (2)
\(\Rightarrow\) \(\frac{b}{5}\) = \(\frac{c}{\frac{25}{4}}\)
Từ (1) và (2) \(\Rightarrow\) \(\frac{a}{3}\) = \(\frac{b}{5}\) = \(\frac{c}{\frac{25}{4}}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{a}{3}\) = \(\frac{b}{5}\) = \(\frac{c}{\frac{25}{4}}\) = \(\frac{a-b+c}{3-5+\frac{25}{4}}\) = \(\frac{34}{\frac{17}{4}}\) = 8
\(\Rightarrow\) \(\begin{cases}a=24\\b=40\\c=50\end{cases}\)