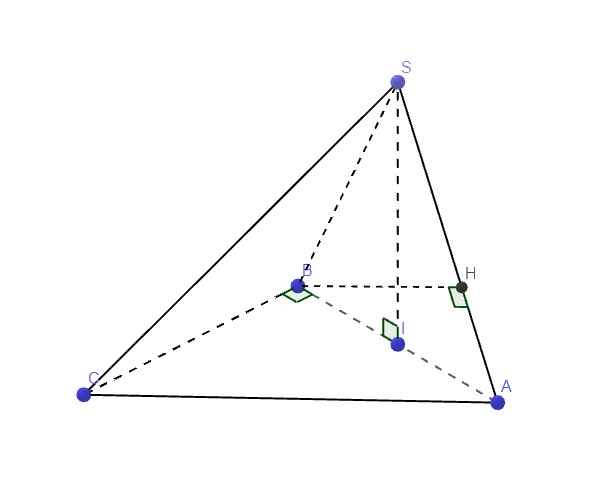
Ta có: \(\left\{{}\begin{matrix}SI\perp\left(ABC\right)\Rightarrow SI\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
Mà \(BC=\left(SBC\right)\cap\left(ABC\right)\)
\(\Rightarrow\widehat{SBA}\) là góc giữa (SBC) và (ABC)
\(\Rightarrow\widehat{SBA}=60^0\)
Trong mp (SAB), từ B kẻ \(BH\perp SA\) (1)
\(BC\perp\left(SAB\right)\) theo cmt \(\Rightarrow BC\perp BH\) (2)
(1);(2) \(\Rightarrow\) BH là đường vuông góc chung của SA và BC
Hay \(BH=d\left(SA;BC\right)\)
\(\Delta SAB\) cân tại S (do SI là trung tuyến đồng thời là đường cao) \(\Rightarrow\widehat{SAB}=\widehat{SBA}=60^0\)
\(\Rightarrow BH=AB.sin60^0=a\sqrt{3}\)