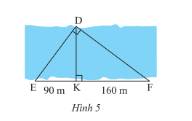
- Xét tam giác \(DEF\) và tam giác \(KDF\) có:
\(\widehat F\) (chung)
\(\widehat {EDF} = \widehat {DKF} = 90^\circ \) (giải thuyết)
Suy ra, \(\Delta DEF\backsim\Delta KDF\) (g.g)
Suy ra, \(\widehat E = \widehat {KDF}\) (hai góc tương ứng).
- Xét tam giác \(DEK\) và tam giác \(FDK\) có:
\(\widehat E = \widehat {KDF}\) (chứng minh trên)
\(\widehat {EKD} = \widehat {FKD} = 90^\circ \) (giải thuyết)
Suy ra, \(\Delta DEK\backsim\Delta FDK\) (g.g)
Suy ra, \(\frac{{DK}}{{FK}} = \frac{{EK}}{{DK}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Suy ra, \(D{K^2} = EK.FK = 90.160 = 14400 \Rightarrow DK = \sqrt {14400} = 120\).
Vậy khoảng cách \(DK = 120m\).
\(DK^2=KE^2+KF^2=8100+25600=33700\)
\(\Rightarrow DK=10\sqrt[]{337}\left(m\right)\)
Đính chính
\(DK^2=KE.KF=90.160=9.16.100\)
\(\Rightarrow DK=3.4.10=120\left(m\right)\)