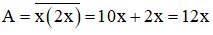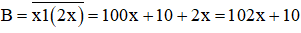Gọi \(x\) là chữ số hàng chục, điều kiện \(0< x\le9\) và \(x\in N\)
Khi đó chữ số hàng đơn vị là \(2x\)
Ta có số đã cho là \(10x+2x\)
Khi xen chữ số 1 vào giữa hai chữ số \(x\) và \(2x\) thì \(x\) trở thành chữ số hàng trăm, còn \(2x\) cũng là chữ số hàng đơn vị. Số mới sẽ là:
\(100x+10.1+2x\)
Vì số mới lớn hơn số cũ đã cho là 370 nên ta có phương trình:
\(100x+10+2x=10x+2x+370\)
Giải phương trình ta được \(x=4\) (nhận). Vậy số ban đầu là 48.
Gọi chữ số hàng chục của số cần tìm là x (x ∈ N; 0 < x ≤ 9).
⇒ Chữ số hàng đơn vị là 2x
⇒ Số cần tìm bằng
Sau khi viết thêm chữ số 1 vào giữa hai chữ số ta được số mới là:
Theo đề bài số mới lớn hơn số ban đầu 370, ta có B = A + 370 nên ta có phương trình
102x + 10 = 12x + 370
⇔ 102x – 12x = 370 – 10
⇔ 90x = 360
⇔ x = 4 (thỏa mãn)
Vậy số cần tìm là 48.