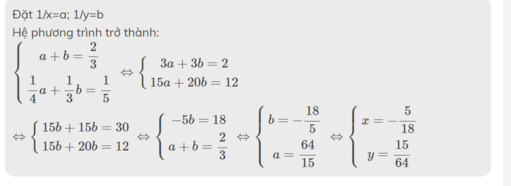Ôn thi vào 10
Các câu hỏi tương tự
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{2}{3}\\\dfrac{1}{4x}+\dfrac{1}{3x}=\dfrac{1}{5}\end{matrix}\right.\)
Giaỉ hệ phương trình này giúp mình vs ạ
Giải hệ phương trình \(\left\{{}\begin{matrix}\sqrt{4x+2}\left(1+\dfrac{1}{x+y+1}\right)=3\\\sqrt{4y+2}\left(1-\dfrac{1}{x+y+1}\right)=1\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x=\dfrac{3}{4}y\\\dfrac{1}{2}\left(x+3\right)\left(y-2\right)-\dfrac{1}{2}xy=9\end{matrix}\right.\)
giải hệ phương trình
Giải hệ phương trình \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\\\dfrac{10}{3x}+\dfrac{10}{y}=1\end{matrix}\right.\)
(mink đag cần gấp)
\(\left\{{}\begin{matrix}^{x^2}+\dfrac{1}{^{y^2}}+\dfrac{x}{y}=1\\\dfrac{x}{y}-2\left(x+\dfrac{1}{y}\right)=-1\end{matrix}\right.\)
Giải Hệ Phương Trình
Giải hệ phương trình:
a) \(\left\{{}\begin{matrix}4x^3+y^2-2y+5=0\\x^2+x^2y^2-4y+3=0\end{matrix}\right.\)
b) \(\left\{{}\begin{matrix}\dfrac{2x^2}{x^2+1}=y\\\dfrac{3y^3}{y^4+y^2+1}=z\\\dfrac{4z^4}{z^6+z^4+z^2+1}=x\end{matrix}\right.\)
giải hệ phương trình \(\left\{{}\begin{matrix}x-y=-1\\\dfrac{2}{x}+\dfrac{3}{y}=2\end{matrix}\right.\)
giải các hệ phương trình
a)\(\left\{{}\begin{matrix}x^2+y^2=1\\x^3+y^3=1\end{matrix}\right.\) b) \(\left\{{}\begin{matrix}\dfrac{1}{x}-\dfrac{1}{y}=\dfrac{5}{12}\\x^2+y^2=1\end{matrix}\right.\)
c)\(\left\{{}\begin{matrix}x^2-xy+y^2=3\\2x^2-xy+3y^2=12\end{matrix}\right.\)
giải hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{2}{x+2}+\dfrac{1}{y+2}=1\\\dfrac{8}{x+2}-\dfrac{5}{y+2}=1\end{matrix}\right.\)