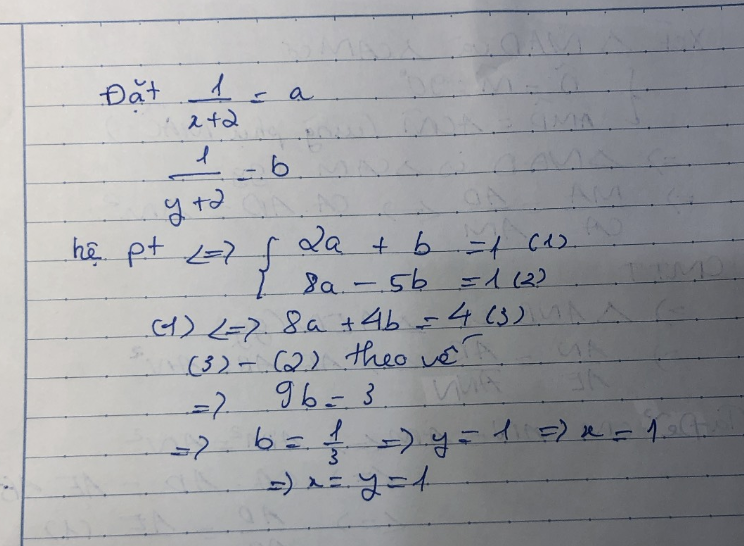Question

giải hệ phương trình:

\(\left\{{}\begin{matrix}\dfrac{2}{x+2}+\dfrac{1}{y+2}=1\\\dfrac{8}{x+2}-\dfrac{5}{y+2}=1\end{matrix}\right.\)

Answer 1

đặt \(\dfrac{1}{x+2}=a,\dfrac{1}{y+2}=b\)(\(x,y\ne-2\))

\(=>\left\{{}\begin{matrix}2a+b=1\\8a-5b=1\end{matrix}\right.=>\left\{{}\begin{matrix}a=\dfrac{1}{3}\\b=\dfrac{1}{3}\end{matrix}\right.\)

\(=>\left\{{}\begin{matrix}\dfrac{1}{x+2}=\dfrac{1}{3}\\\dfrac{1}{y+2}=\dfrac{1}{3}\end{matrix}\right.=>\left\{{}\begin{matrix}x=1\left(tm\right)\\y=1\left(tm\right)\end{matrix}\right.\)

Answer 2

Answer 3

Ta có: \(\left\{{}\begin{matrix}\dfrac{2}{x+2}+\dfrac{1}{y+2}=1\\\dfrac{8}{x+2}-\dfrac{5}{y+2}=1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{8}{x+2}+\dfrac{4}{y+2}=4\\\dfrac{8}{x+2}-\dfrac{5}{y+2}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{9}{y+2}=3\\\dfrac{2}{x+2}+\dfrac{1}{y+2}=1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}y+2=3\\\dfrac{2}{x+2}=1-\dfrac{1}{3}=\dfrac{2}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y+2=3\\x+2=3\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)

Vậy: (x,y)=(1;1)