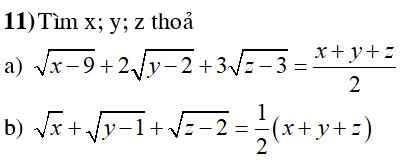a) \(\sqrt[]{x-9}+2\sqrt[]{y-2}+3\sqrt[]{z-3}=\dfrac{x+y+z}{2}\left(1\right)\)
\(Đkxđ:\left\{{}\begin{matrix}x\ge9\\y\ge2\\z\ge3\end{matrix}\right.\)
Áp dụng Bất đẳng thức Bunhiacopxki :
\(\left(1\sqrt[]{x-9}+2\sqrt[]{y-2}+3\sqrt[]{z-3}\right)^2\le\left(1^2+2^2+3^2\right)\left(x-9+y-2+z-3\right)=14\left(x+y+z-14\right)\)
Dấu "=" xảy ra khi và chỉ khi :
\(\dfrac{x-9}{1}=\dfrac{y-2}{2}=\dfrac{z-3}{3}\left(a\right)\)
\(\left(1\right)\Leftrightarrow\)\(14\left(x+y+z-14\right)=\dfrac{\left(x+y+z\right)^2}{4}\left(2\right)\)
Đặt \(t=x+y+z\)
\(\Leftrightarrow14t-196=\dfrac{t^2}{4}\)
\(\Leftrightarrow t^2+56t-784=0\)
\(\Leftrightarrow\left(t-28\right)^2=0\)
\(\Leftrightarrow t=28\)
\(\Leftrightarrow x+y+z=28\)
\(\left(a\right)\Leftrightarrow\dfrac{x-9}{1}=\dfrac{y-2}{2}=\dfrac{z-3}{3}=\dfrac{x+y+z-14}{6}=\dfrac{28-14}{6}=\dfrac{7}{3}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-9=1.\dfrac{7}{3}=\dfrac{7}{3}\\y-2=2.\dfrac{7}{3}=\dfrac{14}{3}\\z-3=3.\dfrac{7}{3}=7\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{34}{3}\\y=\dfrac{20}{3}\\z=10\end{matrix}\right.\)