Bài giải:
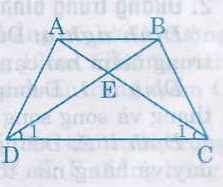
Gọi E là giao điểm của AC và BD.
∆ECD có \(\widehat{C_1}=\widehat{D}\) (do \(\widehat{ACD}=\widehat{BDC}\)) nên là tam giác cân.
Suy ra EC = ED (1)
Tương tự EA = EB (2)
Từ (1) và (2) suy ra AC = BD
Hình thang ABCD có hai đường chéo bằng nhau nên là hình thang cân.
Nối A với C, B với D. Gọi M là giao điểm của AC và BD.
Ta có: \(\widehat{MDC}=\widehat{MCD}\left(gt\right)\)
=> \(\bigtriangleup\)MDC cân tại M
=> MC = MD (1)
Ta lại có: \(\widehat{MAB}=\widehat{MCD}\) (vì hai góc so le trong và AB//CD)
\(\widehat{CDM}=\widehat{ABM}\) (vì hai góc so le trongvà AB//CD)
Mà \(\widehat{CDM}=\widehat{DCM}\left(gt\right)\) nên \(\widehat{MAB}=\widehat{MBA}\)
=> \(\bigtriangleup\) AMB cân tại M
=> MA = MB (2)
Lại có: \(AC=AM+MC\)
\(BD=BM+MD\)
Mà: \(AM=BM\left(cmt\right)\)
\(MC=MD\left(cmt\right)\)
\(\Rightarrow AC=BD\)
=> Hình thang ABCD cân.












