a: A=1/(căn 30+căn 29)
B=1/(căn 29+căn 28)
căn 30+căn 29>căn 29+căn 28
=>A<B
b: C=2*căn 2+căn 3
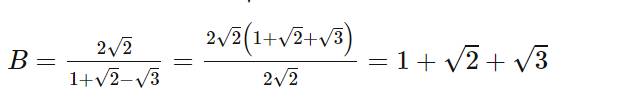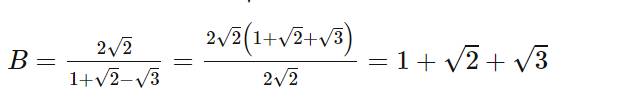=D
C-D=2*căn 2+căn 3-1-căn 2-căn 3=căn 2-1>0
=>C>D
1. Tìm x để biểu thức sau có nghĩa:
a) A= \(\dfrac{x}{x-2}+\sqrt{x-2}\) .
b) B= \(\sqrt{-x^2+2x-1}.\)
2. Giải pt:
a) \(\sqrt{9x^2+6x+1}=\sqrt{11-6\sqrt{2}}.\)
3. Thực hiện phép tính:
a) \(\sqrt{\sqrt{5}-\sqrt{3-\sqrt{29-12\sqrt{5}}}}.\)
b) \(\sqrt{13+30\sqrt{2+\sqrt{9+4\sqrt{2}}}}.\)
Cho A =\(\sqrt{11+\sqrt{96}}\) ;B=\(\dfrac{2\sqrt{2}}{1+\sqrt{2}-\sqrt{3}}\)
So sánh A và B
So sánh:
a, 5+\(\sqrt{ }\)2 và 4+ \(\sqrt{ }\)3
b, \(\)\(\sqrt{ }\)8 - \(\sqrt{ }\)2 và \(\sqrt{ }\)5 - \(\sqrt{ }\)3
c, \(\sqrt{ }\)5 - \(\sqrt{ }\)3 và \(\sqrt{ }\)10 - \(\sqrt{ }\)7
Thực hiện phép tính:
a) \(\sqrt{24+8\sqrt{5}}-\sqrt{9-4\sqrt{5}}.\)
b) \(\sqrt{\sqrt{5}-\sqrt{3-\sqrt{29-12\sqrt{5}}}}\).
c) \(\dfrac{1}{1+\sqrt{2}}+\dfrac{1}{\sqrt{2}+\sqrt{3}}+\dfrac{1}{\sqrt{3}+\sqrt{4}}+....+\dfrac{1}{\sqrt{99}+\sqrt{100}}.\)
rút gọn các biểu thức sau:
a,\(\sqrt{\sqrt{5}-\sqrt{3-\sqrt{29-12\sqrt{5}}}}\)
b,\(\sqrt{6+2\sqrt{5}-\sqrt{29-12\sqrt{5}}}\)
c,\(\sqrt{2+\sqrt{5-\sqrt{13-\sqrt{48}}}}\)
d,\(\left(3-\sqrt{5}\right)\sqrt{3+\sqrt{5}}+\left(3+\sqrt{5}\right)\sqrt{3-\sqrt{5}}\)
Câu 1: Rút gọn biểu thức
a) \(N=\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{48-10\sqrt{7+4\sqrt{3}}}}}\)
b) \(M=\sqrt{5-\sqrt{3-\sqrt{29-12\sqrt{5}}}}\)
Câu 2:
a) Cho a > 0. Chứng minh: \(a+\dfrac{1}{a}\ge2\)
b) Cho \(a\ge0\) , \(b\ge0\) . Chứng minh: \(\sqrt{\dfrac{a+b}{2}}\ge\dfrac{\sqrt{a}+\sqrt{b}}{2}\)
c) Cho a, b > 0. Chứng minh: \(\sqrt{a}+\sqrt{b}\le\dfrac{a}{\sqrt{b}}+\dfrac{b}{\sqrt{a}}\)
d) Chứng minh: \(\dfrac{a^2+2}{\sqrt{a^2+1}}\ge2\) với mọi a
Bài 1:
a) \(\sqrt{13-2\sqrt{42}}\)
b) \(\sqrt{46+6\sqrt{5}}\)
c) \(\sqrt{12-3\sqrt{15}}\)
d) \(\sqrt{11+\sqrt{96}}\)
Bài 2:
a) \(A=\sqrt{6+2\sqrt{2}\sqrt{3-\sqrt{4+2\sqrt{3}}}}\)
b) \(B=\sqrt{5}-\sqrt{3-\sqrt{29-12\sqrt{5}}}\)
c) \(C=\sqrt{3-\sqrt{5}}\left(\sqrt{10}+\sqrt{2}\right)\left(3+\sqrt{5}\right)\)
d) \(D=\sqrt{4+\sqrt{7}}-\sqrt{4-\sqrt{7}}\)
e) \(E=\sqrt{8+2\sqrt{10+2\sqrt{5}}}+\sqrt{8-2\sqrt{10+2\sqrt{5}}}\)
g) \(G=\sqrt{x+2\sqrt{x-1}}+\sqrt{x-2\sqrt{x-1}}\)
h) \(H=4x-\sqrt{9x^2-12x+4}\)
i) \(\frac{\sqrt{7}-\sqrt{2}}{\sqrt{7}+\sqrt{2}}+\frac{\sqrt{7}+\sqrt{2}}{\sqrt{7}-\sqrt{2}}\)
1/Tính
A=\(\dfrac{\sqrt{15-10\sqrt{2}}+\sqrt{13+4\sqrt{10}}-\sqrt{11+2\sqrt{10}}}{2\sqrt{3+2\sqrt{2}}+\sqrt{9-4\sqrt{2}}+\sqrt{12+8\sqrt{2}}}\)
B=\(\dfrac{2+\sqrt{3}}{\sqrt{2}+\sqrt{2}+\sqrt{3}}+\dfrac{2-\sqrt{3}}{\sqrt{2}-\sqrt{2}-\sqrt{3}}\)
C=\(\dfrac{\sqrt{2-\sqrt{3}}+\sqrt{4-\sqrt{15}}+\sqrt{10}}{\sqrt{23-3\sqrt{5}}}\)
D=\(\dfrac{\sqrt{4+\sqrt{3}}+\sqrt{4-\sqrt{3}}}{\sqrt{4+\sqrt{13}}}\)
2/So sánh
\(\sqrt{2017^2-1}-\sqrt{2016^2-1}\) và \(\dfrac{2.1016}{\sqrt{2017^2-1}+\sqrt{2016^2-1}}\)
Tính \(C=\sqrt{13+30\sqrt{2+\sqrt{9+4\sqrt{2}}}}\)
Tính\(D=\sqrt{6+2\sqrt{5-\sqrt{29-12\sqrt{5}}}}\)
rút gọn
\(\sqrt{29+30\sqrt{2+\sqrt{9+4\sqrt{2}}}}+5\sqrt{2}\)
