Gọi x(giờ) và y(giờ) lần lượt là thời gian người thứ nhất và người thứ hai hoàn thành công việc khi làm một mình(Điều kiện: x>16; y>16)
Trong 1 giờ, người thứ nhất làm được: \(\dfrac{1}{x}\)(công việc)
Trong 1 giờ, người thứ hai làm được: \(\dfrac{1}{y}\)(công việc)
Trong 1 giờ, hai người thợ làm được: \(\dfrac{1}{16}\)(công việc)
Do đó, ta có phương trình: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{16}\)(1)
Vì khi người thứ nhất làm trong 3 giờ, người thứ 2 làm trong 6 giờ thì hoàn thành được 25% công việc nên ta có phương trình:
\(\dfrac{3}{x}+\dfrac{6}{y}=\dfrac{1}{4}\)(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{16}\\\dfrac{3}{x}+\dfrac{6}{y}=\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{x}+\dfrac{3}{y}=\dfrac{3}{16}\\\dfrac{3}{x}+\dfrac{6}{y}=\dfrac{1}{4}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{-3}{y}=\dfrac{-1}{16}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{16}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=48\\\dfrac{1}{x}=\dfrac{1}{16}-\dfrac{1}{y}=\dfrac{1}{16}-\dfrac{1}{48}=\dfrac{1}{24}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=24\\y=48\end{matrix}\right.\)(thỏa ĐK)
Vậy: Người thợ thứ nhất cần 24 giờ để hoàn thành công việc khi làm một mình
Người thợ thứ hai cần 48 giờ để hoàn thành công việc khi làm một mình
Gọi thời gian để người thứ nhất và người thứ hai một mình hoàn thành công việc lần lượt là x (giờ) và y (giờ). (Điều kiện x, y > 16).
⇒ Trong một giờ, người thứ nhất làm được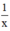 
(công việc); người thứ hai làm được 
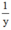(công việc).
+ Cả hai người cùng làm sẽ hoàn thành công việc trong 16 giờ nên ta có phương trình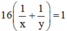 
+ Người thứ nhất làm trong 3 giờ, người thứ hai làm trong 6 giờ thì hoàn thành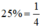 
công việc nên ta có phương trình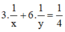 
Vậy ta có hệ phương trình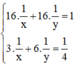 
Đặt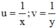 
, hệ phương trình trở thành:
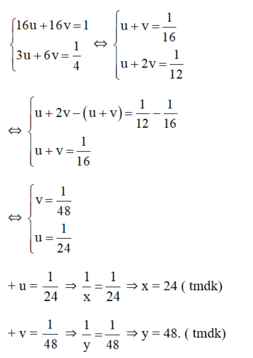
Gợi thời gian người thứ nhất là một mình xong công việc là x (x>16)
Gợi thời gian người thứ hai là một mình xong công việc là y (y>16)
Trong 1 giờ:
-Người thứ nhất làm được:\(\dfrac{1}{x}\)Công việc
-Người thứ hai làm được : \(\dfrac{1}{y}\)Công việc
-Cả 1 người làm được: \(\dfrac{1}{16}\)Công việc
Ta có PT: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{16}\) (1)
-Nếu người thứ nhất làm 3 giờ, người thứ hai làm 6 giờ thì chỉ hoàn thành được 25% công việc nên ta có PT:
\(\dfrac{3}{x}+\dfrac{6}{y}=\dfrac{1}{4}\) (2)
Từ (1) và (2) ta có HPT: \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{16}\\\dfrac{3}{x}+\dfrac{6}{y}=\dfrac{1}{4}\end{matrix}\right.\)⇔\(\left\{{}\begin{matrix}x=24\\y=48\end{matrix}\right.\) (TM)
Vậy người thứ nhất làm môt mình xong công việc trong 24 giờ
Vậy người thứ hai làm một mình xong công việc trong 48 giờ
Gọi thời gian người 1 hoàn thành công việc là x (h); người 2 hoàn thành công việc là y (h) (x; y >0)
1h người 1 làm đc: \(\dfrac{1}{x}\)(công việc) ; 1h người 2 làm đc: \(\dfrac{1}{y}\)(công việc)
1h cả 2 người cùng làm đc là \(\dfrac{1}{16}\)(công việc)
Ta có pt: \(\dfrac{1}{x}\) + \(\dfrac{1}{y}=\text{}\dfrac{1}{16}\)(1)
Nếu 3h người 1 làm đc: \(\dfrac{3}{x}\)(công việc) ; 6h người 2 làm đc: \(\dfrac{6}{y}\)(công việc)
Thì hoàn thành được 25% công việc nên ta có pt sau:
\(\dfrac{3}{x}\) + \(\dfrac{6}{y}\) = 25% <=>\(\dfrac{3}{x}\) + \(\dfrac{6}{y}\) = \(\dfrac{1}{4}\) (2)
Từ (1) và (2) ta có hpt sau: \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{16}\\\dfrac{3}{x}+\dfrac{6}{y}=\dfrac{1}{4}\end{matrix}\right.\)(x; y > 0)
<=> \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{16}\\3\dfrac{1}{x}+6\dfrac{1}{y}=\dfrac{1}{4}\end{matrix}\right.\)
Đặt \(\dfrac{1}{x}\)= a; \(\dfrac{1}{y}\) = b (a; b > 0)
=>\(\left\{{}\begin{matrix}a+b=\dfrac{1}{16}\\3a+6b=\dfrac{1}{4}\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}a=\dfrac{1}{24}\\b=\dfrac{1}{48}\end{matrix}\right.\)(TM)
=> \(\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{1}{24}\\\dfrac{1}{y}=\dfrac{1}{48}\end{matrix}\right.\) <=> x = 24; y = 48 (TMĐK)
Vậy nếu làm riêng thì mỗi người hoàn thành công việc trong 24h và 48h
