Hình học lớp 7
Các câu hỏi tương tự
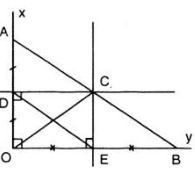
cho góc vuông xoy, điểm A thuộc Ox, điểm B thuộc Oy, đường trung trực của đoạn OA cắt Ox ở D, đường trung trực của đoạn OB cắt Oy tại E. Gọi C là giao điểm của hai đường trung trực đó. Chứng minh rằng:
a) CE = OD b) CE vuông góc CD c) CA = CB d) CA song song DE e) Ba điểm A,B,C thẳng hàng
Cho góc vuông xOy, trên tia Ox lấy điểm A, trên tia Oy lấy điểm B, đường trung trực của đoạn thẳng OA cắt Ox tại D, đường trung trực của đoạn thẳng OB cắt Oy tại E. Gọi C là giao điểm cho 2 đường trung trực. Chứng minh:
a/ OE=OD
b/ \(CE\perp CD\)
c/CA=CB
d/CA // DE
Trên đường trung trực của d của đoạn thẳng AB lấy điểm C bất kì.
a) Chứng minh: Tam giác HAC bằng tam giác BBC. Từ đó suy ra CA = CB ( H là giao điểm của D thuộc d )
b) Trên nửa mặt phẳng không chứa điểm C bờ AB lấy điểm D thuộc d. Chứng minh: Tam giác CAD bằng tam giác CBD.
Qua trung điểm I của đoạn thẳng AB, kẻ đường vuông góc với AB, trên đường vuông góc đó lấy 2 điểm C và D. Nối CA, CB, DA, DB. Tìm các cặp tam giác bằng nhau trong hình vẽ.
Các bạn giúp mình với, giải chi tiết ra giúp mình nhé ! Mình đang gấp nên các bạn làm nhanh giùm mình nha !
Bài 4: Cho tam giác ABC trong đó 2 đỉnh A và C cùng thuộc 1 nửa mặt phẳng bừ là đường trung trực của AB.
Chứng minh rằng: CA<CB.
Giúp với nha các bạn!!
Cho tam giác ABC có góc A bằng 90 độ . Trên tia đối của tia CA lấy D sao cho CD=CA. Trên tia đối của tia CB lấy E sao cho CE=CB . Qua C kẻ đường thẳng d cắt BD lần lượt tại M, N . C/m : C là trung điểm của MN ( chứng minh 2 tao giác bằng nhau theo 2 trường hợp đầu )
1. Cho tam giác ABC cân tại đỉnh A, trung trực của cạnh AC cắt CB tại điểm D ( D nằm ngoài đoạn BC ) trên tia đối tia AD lấy E sao cho AE BD Chứng minh tam giác DCE cân. (Gợi ý: cần chứng minh CD CE)
2. Cho tam giác ABC có. AB AC , lấy điểm E trên cạnh CA sao cho CE BA, các đường trung trực của các đoạn thẳng BE và CA cắt nhau ở I.
a) Chứng minh : ∆AIB ∆CIE.
b) Chứng minh: AI là tia phân giác của góc BAC.
Giúp mình với
Đọc tiếp
1. Cho tam giác ABC cân tại đỉnh A, trung trực của cạnh AC cắt CB tại điểm D ( D nằm ngoài đoạn BC ) trên tia đối tia AD lấy E sao cho AE = BD Chứng minh tam giác DCE cân. (Gợi ý: cần chứng minh CD = CE)
2. Cho tam giác ABC có. AB < AC , lấy điểm E trên cạnh CA sao cho CE = BA, các đường trung trực của các đoạn thẳng BE và CA cắt nhau ở I.
a) Chứng minh : ∆AIB = ∆CIE.
b) Chứng minh: AI là tia phân giác của góc BAC.
Giúp mình với
Cho tam giác ABC có góc A = 110 độ, các đường trung trực của AB và của AC cắt cạnh BC theo thứ tự ở E và F. Tính góc EAF?
Cho tam giác ABC, trong đó 2 đỉnh A và C cùng nửa mặt phẳng cá bờ là đường trung trực của AB. Chứng minh CA < CB.
Cho tam giác ABC và M là một điểm nằm trong tam giác.Gọi I là giao điểm của đường thẳng BM và cạnh AC.
a) So sánh MA với MI + IA, từ đó chứng minh MA + MB < IB + IA.
b) So sánh IB với IC + CB, từ đó chứng minh IB + IA < CA + CB.
c) Chứng minh bất đẳng thức MA + MB < CA + CB.